概要
最適化計算を実施するときには往々にして勾配が必要になりますが、微分の解析解が求められない場合、
- 数値微分をすると計算が遅い
- 自動微分を自分で実装するのは大変
という問題があり、数値微分で妥協するか、よほど問題が大きい時には頑張って自動微分を実装するしかありませんでした。一方で、昨今用いられているディープラーニングで用いられている誤差逆伝播法というのは、実は自動微分(より正しくは、自動微分手法の中のリバースモード蓄積と呼ばれる手法)のことであり、つまりディープラーニングのライブラリを使えば簡単に自動微分が実装できるのでは?と考えました。Chainerはチュートリアルのページで微分計算が簡単にできることをPRしており、これを使って自動微分をしてみたよ、というのが今回の記事です。
Docs » Guides » Variables and Derivatives
題材はあまりいいのが思いつかなかったのですが、前から興味があった、逆行列を最適化計算で求める、というものにしてみました。
勾配取得までの手順
逆行列の計算ですので、環境・評価関数を以下のように考えます。
- 環境は任意の行列Xと、推定中の逆行列Yの積を返す
- 評価関数は、XYとIの差分の要素ごとの2乗和とする
上記のようにすると、評価関数値を最小化するように最適化すれば、XYがIに近づくように、つまりYがXの逆行列となるはずです。
勾配を取得するまでの処理のイメージは以下になります。numpyのarrayをchainerのVariable形式に変換したり、各種処理をchainerの関数で実装することが必要です。
Docs » Reference » Functions
#必要なライブラリをインポートする import numpy as np import chainer from chainer import Variable import chainer.functions as F #任意の3×3の行列を2つ用意する x = np.random.rand(3, 3).astype(np.float32) y = np.random.rand(3, 3).astype(np.float32) #chainerの形式に変換する。(計算グラフが記録されるようになる。) X = Variable(x) Y = Variable(y) #chaierの関数を使って(重要)、行列の積を計算する Z = F.matmul(X, Y) #chainerの関数を使って(重要)、I行列との誤差を計算する E = F.sum(F.absolute(Z - np.eye(Z.shape[0]))) #評価関数値の勾配に任意の値(1)を与えて、backwardファンクションを呼び出す。 E.grad = np.ones_like(E.array) E.backward(retain_grad=True) #Yの勾配が取り出せる grad = Y.grad
勾配の値は、例えばこんな感じです。
print(grad)
array([[ 0.47897792, 0.22566767, 0.05633911],
[-0.2659487 , 1.4563804 , 0.33768457],
[ 1.0298605 , -0.17766836, 0.943027 ]], dtype=float32)
逆行列計算結果
一般的な最急降下法を使って、3×3の逆行列を求めてみました(ソースコードは末尾)。
まず、Xとして乱数で生成した以下を与えました。
print(x)
array([[0.5488135 , 0.71518934, 0.60276335],
[0.5448832 , 0.4236548 , 0.6458941 ],
[0.4375872 , 0.891773 , 0.96366274]], dtype=float32)
また、同様にYの初期値として以下を与えました。
print(before_y)
array([[0.3834415 , 0.79172504, 0.5288949 ],
[0.56804454, 0.92559665, 0.07103606],
[0.0871293 , 0.0202184 , 0.83261985]], dtype=float32)
初期のYはXの逆行列ではないので、積はIにはなりません。
print(np.dot(x, before_y))
array([[0.6692156 , 1.1086732 , 0.84294164],
[0.50586194, 0.8365901 , 0.856065 ],
[0.75831914, 1.1913545 , 1.0971504 ]], dtype=float32)
最適化計算を実施することで誤差が減っていきます。I行列との誤差が0.001以下になったところで計算を止めています。(約1分半。。。)
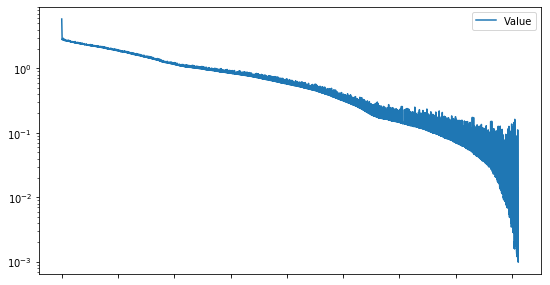
得られたYは以下。
print(after_y)
array([[ 1.99044645, 1.79943597, -2.45138288],
[ 2.87577653, -3.14501214, 0.30953932],
[-3.56536412, 2.09323907, 1.86472368]])
積を計算してみます。
print(np.dot(x, after_y))
array([[ 1.00003780e+00, 3.44761693e-06, 1.42531388e-05],
[ 4.96411722e-05, 1.00009373e+00, -1.65465097e-04],
[-2.74859699e-04, -5.02095241e-05, 1.00030977e+00]])
積はほぼIになっており、Yが逆行列になっていることが分かります。ちなみに、np.linalg.inv使って求めた真のYは以下です。求めたYとほぼ一致していますね。
print(true_y)
array([[ 1.9896084, 1.7991375, -2.4503546],
[ 2.8759089, -3.1447117, 0.3088823],
[-3.5648208, 2.0931487, 1.8645432]], dtype=float32)
Chainerを使った自動微分で逆行列がほぼ正確に求められることを確認できました。
(ただし、やはり普通に掃き出し法等で処理するほうが早いんですね)
まとめ
Chainerの機能を使ってお手軽に自動微分を実装することを思いつき、逆行列を題材に検証を実施しました。結果、自動微分で求めた勾配を使って逆行列を求めることができ、有効性を確認できました。一方で、Chainerの関数を使わないと計算グラフが残らないため、実際のコードをChainerの関数に置き換える部分が多少手間と言えそうです。とはいえ、これを活用すれば、最適化ライフは大きく改善されるのではないでしょうか。
ソースコード
参考までに、本計算の全ソースコードを載せておきます。なお、ChainerはVer4.4.0を使っています。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import time
import chainer
from chainer import Variable
import chainer.functions as F
class Model(object):
def __init__(self, x):
self.x = x
def __call__(self, y):
Y = Variable(y)
Z = F.matmul(x, Y)
self.Y = Y
self.Z = Z
def backward(self, E):
E.grad = np.ones_like(E.array)
E.backward(retain_grad=True)
return self.Y.grad
class Optimizer(object):
def __init__(self, model):
self.model = model
self.alpha_ini = 0.01
self.maxNum = 1000000
self.maxJp = 10000
self.th = 0.001
def evaluate(self, variables):
model = self.model
model(variables)
E = F.sum(F.absolute(model.Z - np.eye(variables.shape[0])))
return E
def optimize(self, variables):
start = time.time()
model = self.model
alpha = self.alpha_ini
maxNum = self.maxNum
maxJp = self.maxJp
th = self.th
elog = pd.DataFrame(index=range(maxNum), columns=['Value', 'alpha'], data=np.NaN)
vlog = pd.DataFrame(index=range(maxNum), columns=range(variables.reshape(-1).shape[0]), data=np.NaN)
glog = pd.DataFrame(index=range(maxNum), columns=range(variables.reshape(-1).shape[0]), data=np.NaN)
E = self.evaluate(variables)
elog.loc[0, :] = float(E.array), alpha
i = 0
j = 0
while i < maxNum:
i += 1
grad = model.backward(E)
variables -= grad * alpha
E = self.evaluate(variables)
if float(E.array) < elog.loc[i-1, 'Value']:
alpha *= 1.2
else:
alpha *= 0.5
elog.loc[i, :] = float(E.array), alpha
vlog.loc[i-1, :] = variables.reshape(-1)
glog.loc[i-1, :] = grad.reshape(-1)
print(i, maxNum, j, maxJp, float(E.array), alpha, time.time()-start)
if float(E.array) < th:
break
if alpha < 10 ** -10:
if j < maxJp:
j += 1
variables += variables * np.random.randn(y.shape[0], y.shape[1]) * 0.1 / j
alpha = self.alpha_ini
else:
break
self.elog = elog.astype(float)
self.vlog = vlog.astype(float)
self.glog = glog.astype(float)
return vlog.loc[elog.iloc[:, 0].idxmin() - 1].values.reshape(variables.shape)
if __name__ == "__main__":
np.random.seed(0)
x = np.random.rand(3, 3).astype(np.float32)
model = Model(x)
y = np.random.rand(3, 3).astype(np.float32)
before_y = y.copy()
model(y)
opt = Optimizer(model)
after_y = opt.optimize(y)
true_y = np.linalg.inv(x)
opt.elog.plot(subplots=True, logy=True)
print(np.dot(x, after_y))
print((np.dot(x, after_y) - np.eye(after_y.shape[0])).sum())