概要

最近プロセスマイニング（Process mining）なるものの書籍が出たという話を聞いて、分野自体がどんなものなのか？のレベルから調べつつ、最もベースとなるアルゴリズムとされていたαアルゴリズムについてロジック概要をまとめ、理解を深めるためにPythonで実装すると共に、ライブラリであるpm4pyを用いて動作検証を実施してみました。

参考文献

以下書籍を読み進めています。

プロセスマイニング　Data Science in Action【電子書籍】[ Wil van der Aalst ]

created by Rinker

アルゴリズム部分だけであれば、以下の論文でも理解できました。
http://www.issj.net/journal/jissj/Vol13_No1_Open/A4V13N1.pdf

プロセスマイニングについて

プロセスマイニングの主目的は、参考書籍にある”イベントログから知識を抽出することで、現実のプロセスを把握、監視、改善すること”であり、実際の作業としてはアルゴルズムを用いてプロセスモデルを得て、その結果を考察していくことであると考えられます。おそらく、データ分析と同様にイベントデータのクレンジングが一番困難であろうことが予想されますね。

イベントログは、イベントのIDや、何時、誰が、何をしたか、というような記録がされているデータを指します。
プロセスマイニングアルゴリズムは、イベントログを入力にプロセスモデルを得るためのものであり、αアルゴリズムやその派生が主要なアルゴリズムとされています。
プロセスモデルは、以下に示すペトリネットのようなイベントログからプロセスを可視化したモデルを指します。ペトリネットはトランジションの集合（T：プロセスで実行されうるタスク：□で表されている）及びプレースの集合（P：プロセスがとりうる状態：〇で表されている）、有向アークの集合（F：状態遷移：矢印で表されている）から構成されていて、トークン（●）の場所で現在プロセスがどこまで完了していて、どこで待ちが発生しているのかを表現することができます。

αアルゴリズムについて

αアルゴリズムのロジックは書籍によれば以下8ステップのシンプルなものであると記載されています。ただ、本分野に精通している人以外は、この内容を見ても私と同じでなかなかついていけないかと思います。（記号が激しすぎる、、、）

そこで、実際実装してみた結果を踏まえて、本アルゴリズムの準備部分も含めてちょっと乱暴に手順を簡略化してみました。

イベントログデータを走査し、トランジションの一覧、及び前後関係をリストアップする。（アルゴリズムの1, 2, 3, 及び4の一部に対応）
リストアップした前後関係をマトリックス上に整理（足跡（Foot print）行列と呼ぶ）し、片方向の前後関係しかないトランジションの組、双方向の前後関係があるトランジションの組、前後関係が確認できなかったトランジションの組に分類して整理する。（アルゴリズムの4のメインに対応）
2.で整理した情報から、ペトリネットを表現するために必要な、プレースの集合、アークの集合を抽出する。（アルゴリズムの4の一部、5, 6, 7, 8に対応）

1.では、ログが直接前後しているデータしか関係を見ないようになっていて、2つ以上後、2つ以上前に出てくるトランジションは関係があるとは見なさないことが重要です。このことから、ログに直接の関係ない2つ以上のプロセスが混在している（例えば、ウェブサーバーでほぼ同時に利用した利用者AとBのログ）ようなケースにはそのままは使えない（利用者でログを分ける前処理が必要）ことが想像できます。

2.では、トランジションを行列の要素に取った、以下図に示すような足跡行列を作成します。以下の例では、L2というログに対する足跡行列が示されています。一例をあげると、ログの中にa→aの遷移はないので(a, a)は#（前後関係なし）、a→bの遷移はあるが、b→aの遷移はないので(a, b)は→、(b, a)は←（片方向の関係）、c→dもd→cもあるので、(c, d)及び(d, c)は||（両方向の前後関係）となっています。起きたか／起きなかったか、であり回数には着目されていないため、前処理しないと偶然起きたケースも紛れ込むことには注意した方がよさそうです。

3.の内容は言葉では説明しがたいのですが、ペトリネットを表現する上での約束事を満たすように処理する必要があります。論理式を追っていくと以下のようなことを行う必要があることが読み取れます。具体的には次章の実装部分を見ていただくのが良いと思います。

トランジションTLの各要素を非復元抽出して全ての部分集合の組を抽出する
1.で得た部分集合の中で、部分集合の中に#の関係でないトランジションの組み合わせがあるものを削除する
2.で得た部分集合から2つを選んだ組み合わせをすべて抽出し、1つ目を遷移元、2つ目を遷移先とし、それぞれについて足跡行列上で→の関係でないものを削除する（ここまでで、XLが求まる）
XLの各要素のうち、遷移元と遷移先の両方が他の要素の部分集合となっているものを削除する（ここまでで、YLが求まる）
YLに開始と終了のプレースを追加したものをPLとする。
TLとPLを結ぶすべてのアークを定義してFLとする。

αアルゴリズムを実装

ステップ１：イベントログデータを走査し、トランジションの一覧、及び前後関係をリストアップするまで

上記の内容を踏まえてαアルゴリズムを実装していきます。まず必要なライブラリをインポートすると共に、例となるログ（L)を作成します。このログは参考文献のL1と同じです。

#必要なライブラリのインポート
import pandas as pd
import numpy as np
from itertools import combinations, permutations
import pydotplus
#ログを定義
L = [["a", "b", "c", "d"]]*3 + [["a", "c", "b", "d"]]*2 + [["a", "e", "d"]]

次に、トランジションの一覧、最初のトランジションの一覧、最後のトランジションの一覧を取得します。

df_L = pd.DataFrame(L).T
TL = pd.melt(df_L)['value'].dropna().unique().tolist()
TI = df_L.iloc[0].unique().tolist()
TO = df_L.fillna(method='ffill').iloc[-1].unique().tolist()

df_Lは以下図のように行方向がログの流れ、列方向がログのN数を表しています。

TL、TIとTOは以下のようになります。TLは全ての記号であるa～eが、TIは最初になったことがあるaが、TOは最後になったことがあるdが選ばれており、正しい動作となっています。

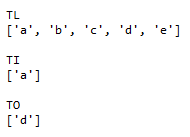
続いて、ログの直接の前後関係を取得します。以下では、df_Lをmeltで整形して1行ずらしで結合（1行目）し、異なるログID間の前後関係を評価しないよう、ログのIDが一致するものだけを取り出した処理（2行目）を実施しています。

df_Dp = pd.concat([pd.melt(df_L), pd.melt(df_L).shift()], axis=1)   
df_Dp = df_Dp.loc[df_Dp.iloc[:, 0] == df_Dp.iloc[:, 2], 'value'].dropna()
df_Dp.columns = ['y', 'x']

得られたdf_Dpはこんな感じです。df_Lと比較すれば、正しく前後関係が取得できていることが確認できます。

ステップ２：リストアップした前後関係をマトリックス上に整理して分類するまで

次に、トランジションの3種類の前後関係（片方向、双方向、関係なし）の分類をして足跡行列を作ります。以下は、まず、1行目でdf_Dpを縦軸横軸それぞれにトランジションを取ったピボットテーブルを作成し、その後足跡行列であるdf_Footprintを作成しています。df_Footprintは初期値をすべて＃（関係なし）として、df_Dp_pivotとdf_Dp_pivotの転置行列の各要素が正かどうかをみることで関係の向きを算出しています。

df_Dp_pivot = df_Dp.reset_index().pivot_table(index='x', columns='y', aggfunc='count', values='index').reindex(TL).reindex(TL, axis=1).fillna(0)
df_Footprint = pd.DataFrame(index=TL, columns=TL, data='#')
df_Footprint[(df_Dp_pivot&gt;0)&amp;(df_Dp_pivot.T&lt;=0)] = '→'
df_Footprint[(df_Dp_pivot.T&gt;0)&amp;(df_Dp_pivot&lt;=0)] = '←'
df_Footprint[(df_Dp_pivot&gt;0)&amp;(df_Dp_pivot.T&gt;0)] = '||'

得られた足跡行列は以下です。その下にある正解の表と比較して内容が一致していることが分かります。

表のままだとこの先で少し使いにくいので、df_Dpのように行方向に関係が並んだ形式での変数も作っておきます。

#df_Dpから重複を除外
df_Dp_unique = df_Dp.drop_duplicates()
#片方向の関係を抽出
df_Dp_onepath = df_Dp_unique.loc[~df_Dp_unique[['x', 'y']].sum(axis=1).isin(df_Dp_unique[['y', 'x']].sum(axis=1))]
#双方向の関係を抽出
df_Dp_parallel = df_Dp_unique.drop(df_Dp_onepath.index)

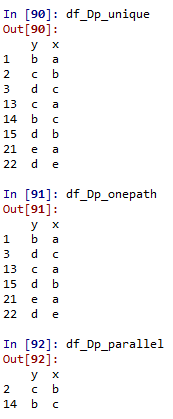
出来上がった変数の中身はこんな感じです。df_Dp_onepathとdf_Dp_parallelの要素を加えるとdf_Dp_uniqueになります。

ステップ３：ペトリネットを表現するために必要なプレース／アークの集合を抽出するまで

ここからはややこしさが増していきますが、順に追っていけば大丈夫だと思います。

ステップ３－１：トランジションTLの各要素を非復元抽出して全ての部分集合の組を抽出する

まず、TLの各要素（a, b, c, d, e)を使って得られる全ての部分集合の組み合わせを作ります。関数は参考サイト様から使わせていただきました。

def get_subsets(items):
    """
    # 全ての部分集合の列挙
    
    """
    subsets=[]
    for i in range(len(items) + 1):
        for c in combinations(items, i):
            subsets.append(set(c))
            
    return subsets

TL_subsets = get_subsets(TL)

具体的に得られたものを見たいただいた方がイメージしやすいかもしれません。

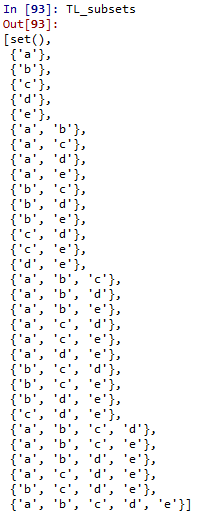
ステップ３－２：部分集合の中に#の関係でないトランジションの組み合わせがあるものを削除する

TL_subsetsの中に、aとbなど片方向（または双方向）の関係を持ったトランジションを両方含んでいるものが多数あります。これらを含まないTL_subsets_independentを作成します。

TL_subsets_independent = []
# #関係のものだけを含む集合を取り出す
for subset in TL_subsets:
    #空集合は除外
    if len(subset) == 0:
        continue
    #要素数1のものは採用
    if len(subset) == 1:
        TL_subsets_independent.append(subset)
        continue
    #要素数が2以上のものについて、df_Dp_uniqueに該当するものがないものだけを抽出
    judge = 0
    for i in df_Dp_unique.index:
        judge += (subset &gt;= set(df_Dp_unique.loc[i]))
    if judge == 0:
        TL_subsets_independent.append(subset)

これも得られたものを見た方が分かり易そうです。

TL_subsets_independent

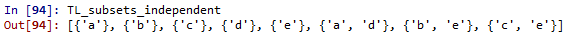
ステップ３－３：2で作った部分集合から2つを選んだ組み合わせをすべて抽出し、1つ目を遷移元、2つ目を遷移先とし、それぞれについて足跡行列上で→の関係でないものを削除する

TL_subsets_independentから2つを選び、それらの部分集合を構成するトランジションについて、1つ目で選んだものと2つ目で選んだものの間に→の関係があるものを抽出してXLとします。

#独立した部分集合同士の組み合わせから、df_Dp_onepathに関係があるものだけを抽出
XL = []
for subset_from in TL_subsets_independent:
    for subset_to in TL_subsets_independent:
        judge_XL = True
        for mem_from in subset_from:
            for mem_to in subset_to:
                if ((df_Dp_onepath['x'] == mem_from) &amp; (df_Dp_onepath['y'] == mem_to)).sum() == 0:
                    judge_XL = False
                    break
            if judge_XL == False:
                break
        if judge_XL == True:
            XL.append([subset_from, subset_to])

これもXLを直接見た方が分かり易そうです。参考文献で示されている結果と比較すると一致していることが確認できます。

参考文献より引用

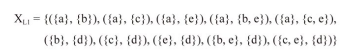
ステップ３－４：XLの各要素のうち、遷移元と遷移先の両方が他の要素の部分集合となっているものを削除する

XLの各要素について、他の要素で含まれているもの（例えば({a}, {b})は({a}, {b, e})に含まれている）を除外していきます。

#XLの中から最大ペアだけを抽出
YL = []
for X1 in XL:
    judge_YL = 0
    for X2 in XL:
        if (X2[0] &gt;= X1[0]) &amp; (X2[1] &gt;= X1[1]):
            judge_YL += 1
        if judge_YL &gt; 1:
            break
    if judge_YL == 1:
        YL.append(X1)

冗長な成分を削除すると、4つまで減っています。

ステップ３－５：YLに開始と終了のプレースを追加したものをPLとする

ここからは簡単です。PLはYLに最初と最後を追加すればOKです。

PL = YL.copy()
PL.extend(['iL', 'oL'])

ステップ３－６：TLとPLを結ぶすべてのアークを定義してFLとする

FLは、YLの各メンバーとプレースを結ぶアーク、及びiLとTI, TOとoLを結ぶアークで構成されます。

FL = []
for Yi in YL:
    for mem_from in Yi[0]:
        FL.append([mem_from, Yi])
    for mem_to in Yi[1]:
        FL.append([Yi, mem_to])
for Ti in TI:
    FL.append(['iL', Ti])
for To in TO:
    FL.append([To, 'oL'])

最終ステップ：ペトリネットを描画するまで

ここまででペトリネットの描画に必要なTL, PL, FLを作成することができました。ペトリネットを作成する使いやすいコードが見つけられなかったので、過去記事を参考にサクッと自作してみました。

def petriViz(TL, PL, FL, fileName='petrinet.png'):
     
    #オブジェクトを定義
    graph = pydotplus.Dot(graph_type='digraph')
    graph.set_rankdir('LR')
     
    #ノードを追加
    Node_name = {}
    for t in TL:
        node = pydotplus.Node(str(t), shape='square')
        graph.add_node(node)
        Node_name[str(t)] = node.get_name()
        
    #ノードを追加
    for i, p in enumerate(PL):
        if len(str(p)) &gt; 6:
            label = 'P' + str(i)
        else:
            label = str(p)
        node = pydotplus.Node(label, shape='circle')
        graph.add_node(node)
        Node_name[str(p)] = node.get_name()
     
    #エッジを追加  
    for f in FL:
        edge = pydotplus.Edge(graph.get_node(Node_name[str(f[0])])[0], graph.get_node(Node_name[str(f[1])])[0])
        graph.add_edge(edge)
 
    #グラフ描画                
    graph.write_png(fileName, prog='dot')

petriViz(TL, PL, FL)

得られたペトリネットがこちら。書籍と同じものが得られていることを確認できました。

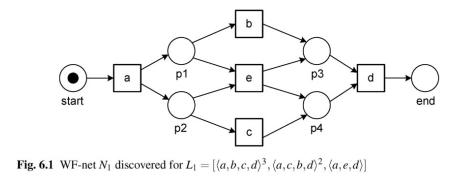
また、ログを別のもの（参考文献内でL2としているもの）に置き換えて動作させてみました。

L = [["a", "b", "c", "d"]]*3 + [["a", "c", "b", "d"]]*4 + [["a", "b", "c", "e", "f", "b", "c", "d"]]*2 + 
    [["a", "b", "c", "e", "f", "c", "b", "d"]] + [["a", "c", "b", "e", "f", "b", "c", "d"]]*2 + 
    [["a", "c", "b", "e", "f", "b", "c", "e", "f", "c", "b", "d"]]

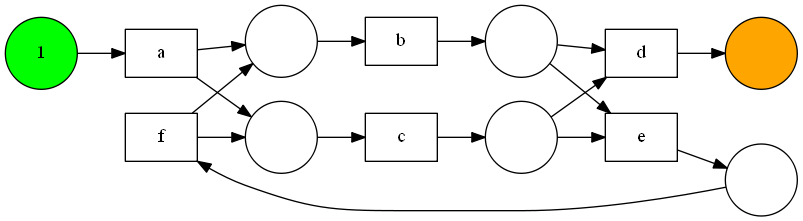
得られた結果がこちら。文献の結果（fig6.2）と比較すると、形やpの番号は違うのですが、初めにaがあり２つのpに分岐しそこからbとcへ接続して、、、と接続関係自体は合っていたため、ロジックの実装は正しくgraphVizの出力だけの問題であることが分かります。逆に言うと、表示の部分まで作りこむのはかなり大変だなと感じました。

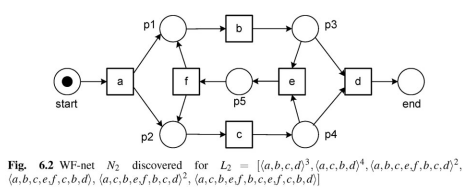
ライブラリ（pm4py）を用いた動作検証

記事がだいぶ長くなってきていますが、αアルゴリズムをほぼ完全に理解できたところでライブラリを使った動作を検証していきます。ライブラリのインストールは下記でOKです。バージョンは1.2.4を使っています。

pip install pm4py

結構使うまでが難しい印象ですが、サンプルコードを眺め、スクリプトをデバッグモードで追いかけながら読み解くと、次のコードでとりあえず動作させられることが分かりました。

import pandas as pd
import datetime
from pm4py.algo.discovery.alpha import factory as alpha_miner
from pm4py.visualization.petrinet import factory as vis_factory

L = [["a", "b", "c", "d"]]*3 + [["a", "c", "b", "d"]]*2 + [["a", "e", "d"]]
dfs_L = []
for i, l in enumerate(L):
    tdf = pd.DataFrame(data=l, columns=['concept:name'])
    tdf['case:concept:name'] = i
    tdf['time:timestamp'] = datetime.datetime(2019, 1, 1)
    
    dfs_L.append(tdf)
df_L = pd.concat(dfs_L).reset_index(drop=True)    

net, initial_marking, final_marking = alpha_miner.apply(df_L)
gviz = vis_factory.apply(net, initial_marking, final_marking)
vis_factory.view(gviz)

ログをPandasのデータフレームに整形できれば、あとは適当に投げ込んで使えます。一応、graphVziのdot.exeがコマンドプロンプト上で動作するようにパスを通しておく必要があります。

データフレームでは、最低限「case:concept:name」というログIDを表す列、「concept:name」というトランジションを表す列、「time:timestamp」というタイムスタンプを表す列が必要でした。ただし、タイムスタンプは適当でもとりあえず動作しています。

動作させて得られた結果がこちら。L1は実装同様に綺麗にかけています。L2は実装したものよりは分かり易いですが、書籍のもののようには書いてくれないようです。この辺りはライブラリを使っても簡単ではないのかもしれませんね。

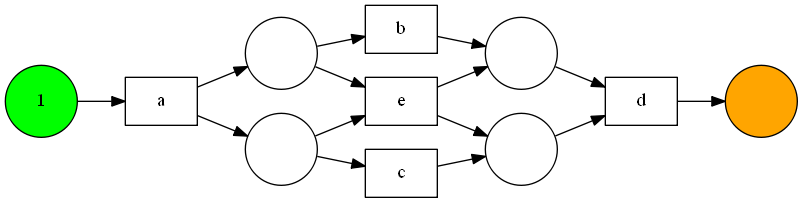
まとめ

αアルゴリズムについてロジック概要をまとめ、理解を深めるためにPythonで実装すると共に、ライブラリであるpm4pyを用いて動作検証を実施してみました。実装したこともありαアルゴリズムはほぼ完全に理解できたように思います。今後は、実際のログデータを用いての分析や、αアルゴリズム以外のロジックの検討も進めていこうと思います。