概要
Preferred Networks社が提供する深層学習ツールである chainerを使ってLSTM(Long Short Term Memory)を学習する手順を整理しました。LSTMはメモリセルと呼ばれる配列要素を持っており、そこへのデータ入出力等をNNの最適化要素に加えることで時系列的な概念の学習を可能としています。このため、通常のNNを学習する場合と比べて以下を追加で検討する必要があります。本記事では、整理した内容を元に必要機能のクラス化・ファンクション化を行うと共に、簡単なサンプルデータを用いた検証を実施しました。なお、Chainerはversion2.0.2を使っています。
- LSTMを含んだモデルの検討
- 時系列的な連続性を考慮したイテレータの検討
- 時系列的な連続性を考慮した学習手法の検討
- 時系列的な連続性を考慮した検証手法の検討
- 時系列的な連続性を考慮した予測方法の検討
上記は時系列を含めた目的変数や説明変数の構成に大きく影響を受けるため、本記事では以下のような「全入力変数に対して、次の時刻の値を予測する多入力・多出力モデル」を対象としています。このようにすることで、出力を再度入力としてLSTMに投入して次の時刻を予測することができるため、再帰的にどこまでも先の予測をすることが可能になります。(要は使い勝手が良い)

ソースコードは以下で公開しています。
https://github.com/Rosyuku/lstm.git
gitが分からないという方はこちらからどうぞ。
lstm.zip (607 ダウンロード)
通常のNNを学習する手順は以下記事で整理しているので、参考にしてみてください。
LSTMの動作の中身を理解したい、という場合は以下記事で整理しているので、参考にしてみてください。
Kerasを使った場合も整理してみました。
LSTM用の機能の組込み
概要で述べた5項目について具体的に処理内容を記載していきます。
LSTMを含んだモデルの検討
以下にLSTMを含んだモデルの例を示します。例では、3段の全結合NNの2段目がLSTM接続を持っています。基本的には通常のNNと同じですが、reset_stateというファンクションが定義されていることに気が付くと思います。これは、上述したLSTMのメモリセルを初期化する(ゼロクリアする)もので、基本的には学習や検証・予測を問わずLSTMモデルを初期化する時には必ず実行します。
class Model(Chain):
def __init__(self, n_input, n_output, n_units):
super(Model, self).__init__(
l1 = L.Linear(n_input, n_units),
l2 = L.LSTM(n_units, n_units),
l3 = L.Linear(n_units, n_output),
)
def reset_state(self):
self.l2.reset_state()
def __call__(self, x):
h1 = self.l1(x)
h2 = self.l2(h1)
o = self.l3(h2)
return o
時系列的な連続性を考慮したイテレータの検討
次に学習・検証時に使うイテレータについてです。通常のNNでは各データレコードはiid(独立)と見なしていましたが、LSTMでは時間的な連続性を考慮したいので、時系列的に順番にデータが出てくる必要があり、内部処理としては大きく以下の2つを組み込む必要があります。現状ではこれは手でコーディングするしかないようです。
- loop(イテレータが呼び出された回数)が0の時、batch_sizeに応じたデータのインデックスをランダムに選んで(offsets)返す。検証の場合(repeatがfalse)はすべてを返す。ただし、n回分の連続性を学習させる場合はその分の余裕が出るように制約を設ける。
- offsetsとloopに応じた入出力データを返す。入力データをtとすると、出力データは1コマ先(pred)となる。
以下にイテレータの例を示します。__next__ファンクションが、次のデータを呼び出す時に使うものです。
class LSTM_Iterator(chainer.dataset.Iterator):
def __init__(self, dataset, batch_size=10, seq_len=10, support_len=10, repeat=True, pred=1):
self.seq_length = seq_len
self.support_len = support_len
self.dataset = dataset
self.nsamples = dataset.shape[0]
self.columns = dataset.shape[1]
self.pred = pred
self.batch_size = batch_size
self.repeat = repeat
self.epoch = 0
self.iteration = 0
self.loop = 0
self.is_new_epoch = False
def __next__(self):
#1
if self.loop == 0:
self.iteration += 1
if self.repeat == True:
self.offsets = np.random.randint(0, self.nsamples-self.seq_length-self.pred-1, size=self.batch_size)
else:
self.offsets = np.arange(0, self.nsamples-self.seq_length-self.pred-1)
#2
x, t = self.get_data(self.loop)
self.epoch = int((self.iteration * self.batch_size) // self.nsamples)
return x, t
def get_data(self, i):
x = self.dataset[self.offsets+i, :]
t = self.dataset[self.offsets+i+self.pred, :]
return x, t
def serialze(self, serialzier):
self.iteration = serialzier('iteration', self.iteration)
self.epoch = serialzier('epoch', self.epoch)
@property
def epoch_detail(self):
return self.epoch
時系列的な連続性を考慮した学習手法の検討
次に学習処理についてです。再帰的な運用による学習を進めるため、次コマを予測した結果をそのまま次の入力として使います。ただし、ある程度モデルの精度が上がってくる前にこの方法を使うと、学習がうまくいかなくなる可能性が高いため、最小のnコマ(support_len)の間は予測結果ではなく真値を次の入力にするようにします。予測結果と真値の関係から誤差を計算し、その誤差を元にパラメータを更新するところは通常のNNと同じとしました。以下に例を示します。
class LSTM_updater(training.StandardUpdater):
def __init__(self, train_iter, optimizer, device):
super(LSTM_updater, self).__init__(train_iter, optimizer, device=device)
self.seq_length = train_iter.seq_length
self.support_len = train_iter.support_len
def update_core(self):
loss = 0
train_iter = self.get_iterator('main')
optimizer = self.get_optimizer('main')
optimizer.target.predictor.reset_state()
for i in range(self.seq_length):
train_iter.loop = i
x, t = train_iter.__next__()
if i == self.support_len:
y = optimizer.target.predictor(x)
if i <= self.support_len:
loss += optimizer.target(x, t)
else:
loss += optimizer.target(y, t)
y = optimizer.target.predictor(y)
optimizer.target.zerograds()
loss.backward()
loss.unchain_backward()
optimizer.update()
時系列的な連続性を考慮した検証手法の検討
検証では、test_iterの全条件について予測を実施し精度を評価します。複数の目的変数があるため、それぞれの変数についての誤差(RMSE)と全変数の誤差の平均を評価することとしています。以下に関数の例を示します。
def valid(model, test_iter, total='Total', s=0):
model.reset_state()
res1 = pd.DataFrame(index=range(test_iter.seq_length), columns=range(test_iter.columns), data=pd.np.NaN)
res2 = pd.DataFrame(index=range(test_iter.seq_length), columns=[total], data=pd.np.NaN)
for i in range(test_iter.seq_length):
test_iter.loop = i
x, t = test_iter.next()
if i <= s:
y = model(x)
else:
y = model(y)
res1.iloc[i, :] = ((y - t)**2).data.mean(axis=0)**0.5
res2.iloc[i, 0] = ((y - t)**2).data.mean()**0.5
res = pd.concat([res1, res2], axis=1)
res.index += 1
return res
時系列的な連続性を考慮した予測方法の検討
予測ではデータのない将来を対象とする必要があるため、以下のように真値がある場合とない場合に分けて処理を変えています。また、全体の誤差ではなく1回の予測の値が具体的に得られるように作っています。以下の例では、真値がres2に、予測値がres1に入っています。
def pred(model, data, seq, s=0, diff=1):
model.reset_state()
res1 = pd.DataFrame(index=range(seq), columns=range(data.shape[1]), data=pd.np.NaN)
res2 = pd.DataFrame(index=range(seq), columns=range(data.shape[1]), data=pd.np.NaN)
for i in range(seq):
if i <= s or i==0:
x = data[[i]]
x = model(x)
res1.iloc[i] = x.data
if data.shape[0] > i + diff:
res2.iloc[i] = data[[i+diff]]
return res1, res2
サンプル(Sine波とCos波)を対象とした動作検証
以下に示すようなSine波とCos波(周波数2倍)を使って動作検証を実施しました。画像は上が学習データ、下が検証データです。動作検証のため、できて当たり前のデータとしました。
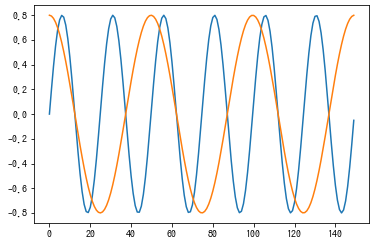

これを100エポック学習させた時のログがこちら。学習とともに学習誤差が減っており、きちんと動いていそうです。
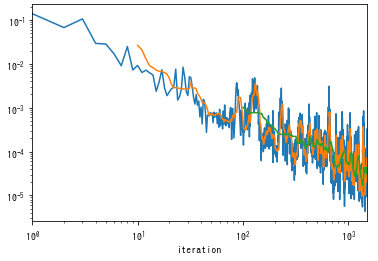
次に検証を実施した場合がこちら。縦軸が誤差(RMSE)で横軸が再帰予測の繰り返し回数を表しています。再帰予測を繰り返して時系列が先の予測をしようとするほど誤差が増加する傾向があります。一方で学習とともに誤差が低減している傾向が読み取れます。これより、汎化誤差が減少していることを確認でき、検証も正しく動いていると言えそうです。
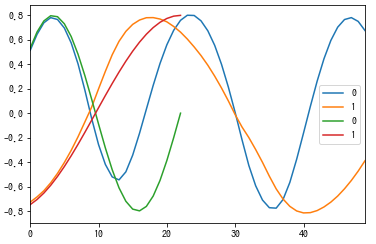
最後に予測を実施した結果を示します。縦軸はSine波とCos波の値で、横軸が時系列を表しています。一致はしておらずまだ学習が不足している傾向ですが、Sine波とCos波の概形は学習できています。また、真値がない先(25以降)も未知の領域を再帰的に予測できています。これより、予測も正しく動いていると言えそうです。
まとめ
chainerを使ってLSTMを学習する手順を整理し、整理した内容を元に必要機能のクラス化・ファンクション化を行うと共に、簡単なサンプルデータを用いた検証を実施しました。LSTMは人気の手法ですが使うまでが少し手間と感じますので、本記事が皆様のお役に立てれば何よりです。