概要

以下の記事でChainerを使った場合のLSTMを学習する手順を整理しましたが、本記事ではKerasを使った場合について同様に整理してみました。結論から言うと、単純にLSTMを使いたい、と言うニーズであればKerasの方がかなりお手軽でした。

kerasを使ってLSTMを使うまでの流れ

まずはtensorflowとkerasをインストールします。

pip install tensorflow
pip install keras

次にkerasのLSTMに投げ込むデータセットを作成します。おそらくここが唯一分かりにくい部分ですので、絵を書いてみました。左側が元データ、右側がkerasのLSTMが必要とするデータの形式です。kerasのLSTMでは、左の列から右の列に向けてデータをLSTMに投入していき、一番右の列が出力として得られる仕様になっているようです（return_sequences=Falseとした場合）。従って、元データを下の絵のように変換した後、学習時はfitに一番右の列を除くデータを説明変数、一番右の列を目的変数として与えて使うことになります。

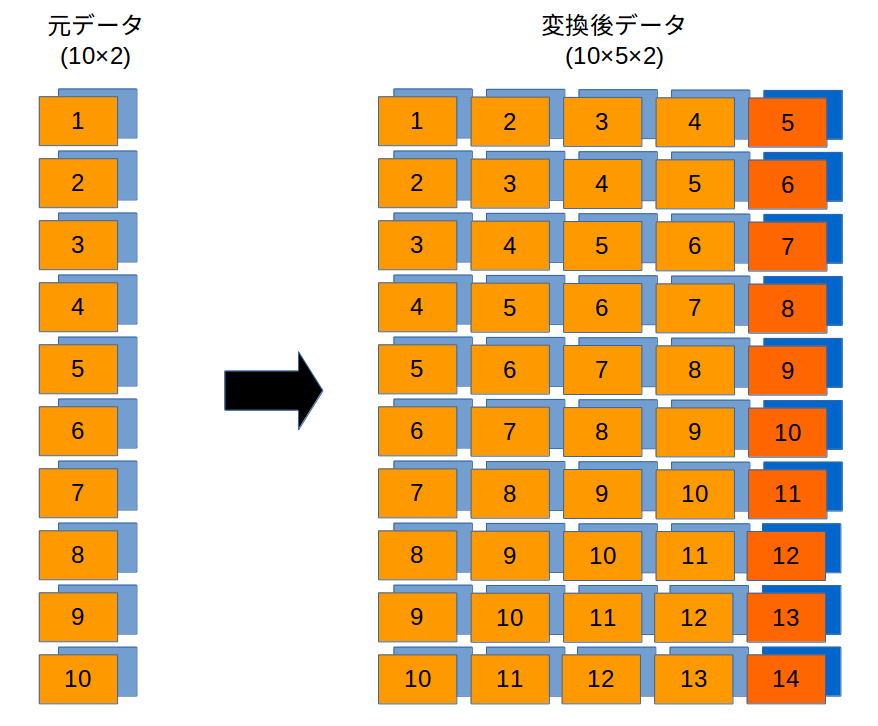
以下が、sin波とcos波を例とした場合のサンプルコードです。timestepsという変数が列数を表しています（上の絵で5になっているもの）。lstm_data_xが上絵右の色が薄い部分（説明変数）、lstm_data_yが同色が濃い部分（目的変数）になります。多分、パラメータを変えれば他のデータでも動作すると思います。

def sincos(T=100):
   x = np.arange(0, 2*T+1)
   return np.concatenate([np.sin(2.0 * np.pi * x / T).reshape(-1, 1), np.cos(2.0 * np.pi * x / T).reshape(-1, 1)], axis=1)

if __name__ == "__main__":

   #データセット作り
   data = sincos()

   timesteps = 10
   data_dim = data.shape[1]

   lstm_data = []
   index_data = []

   for i in range(timesteps):

       length = data[i:-1].shape[0] // timesteps
       lstm_data.append(data[i:i+length*timesteps].reshape(length, timesteps, data_dim))
       index_data.append(np.arange(i, i+(length*timesteps), timesteps))

   lstm_data = np.concatenate(lstm_data, axis=0)
   index_data = np.concatenate(index_data, axis=0)
   lstm_data = lstm_data[pd.Series(index_data).sort_values().index]

   lstm_data_x = lstm_data[:, :-1, :]
   lstm_data_y = lstm_data[:, -1, :]

ここから先は簡単で、モデルの定義、学習、予測、と進みます。

   #モデル定義
   model = Sequential()
   model.add(LSTM(hidden, input_shape=(timesteps-1, data_dim), stateful=False, return_sequences=False))
#    model.add(BatchNormalization())
   model.add(Dense(data_dim))
   model.compile(loss="mean_squared_error", optimizer='adam')

   #学習
   model.fit(lstm_data_x, lstm_data_y,
             batch_size=32,
             epochs=20,
             validation_split=0.1,
             )

   #保存と読み込み
   model.save("sincos_model.h5")
   load_model = load_model("sincos_model.h5")

   #予測
   lstm_data_y_predict = model.predict(lstm_data_x)

ひと手間かかりますが、再帰的な予測をする使い方もちゃんとできます。

    #再帰予測
   lstm_data_future = pd.DataFrame(index=range(300), columns=['sin', 'cos'], data=0)
   lstm_data_future.iloc[:timesteps-1, :] = lstm_data_x[-1, :, :]

   for i in lstm_data_future.index[timesteps-1:]:

       x = lstm_data_future.iloc[i-timesteps+1:i, :].values.reshape(1, timesteps-1, -1)
       y = model.predict(x)
       lstm_data_future.iloc[[i], :] = y

まとめ

LSTMを使うという視点で考えると、Chainerに比べて遥かに簡単という印象です。用途に応じて使い分けていかないといけないですね。

ソースコード

以下にソースコード全文を載せておきます。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

from sklearn.datasets import load_iris

from keras.models import Sequential, load_model
from keras.layers.core import Dense, Activation
from keras.layers import BatchNormalization
from keras.layers.recurrent import LSTM
from keras.utils import np_utils
from keras.optimizers import Adam

def sin(T=100):
   x = np.arange(0, 2*T+1)
   return np.sin(2.0 * np.pi * x / T).reshape(-1, 1)

def sincos(T=100):
   x = np.arange(0, 2*T+1)
   return np.concatenate([np.sin(2.0 * np.pi * x / T).reshape(-1, 1), np.cos(2.0 * np.pi * x / T).reshape(-1, 1)], axis=1)

if __name__ == "__main__":

   #データセット作り
   data = sincos()

   timesteps = 10
   hidden = 100
   data_dim = data.shape[1]

   lstm_data = []
   index_data = []

   for i in range(timesteps):

       length = data[i:-1].shape[0] // timesteps
       lstm_data.append(data[i:i+length*timesteps].reshape(length, timesteps, data_dim))
       index_data.append(np.arange(i, i+(length*timesteps), timesteps))

   lstm_data = np.concatenate(lstm_data, axis=0)
   index_data = np.concatenate(index_data, axis=0)
   lstm_data = lstm_data[pd.Series(index_data).sort_values().index]

   lstm_data_x = lstm_data[:, :-1, :]
   lstm_data_y = lstm_data[:, -1, :]

   #モデル定義
   model = Sequential()
   model.add(LSTM(hidden, input_shape=(timesteps-1, data_dim), stateful=False, return_sequences=False))
#    model.add(BatchNormalization())
   model.add(Dense(data_dim))
   model.compile(loss="mean_squared_error", optimizer='adam')

   #学習
   model.fit(lstm_data_x, lstm_data_y,
             batch_size=32,
             epochs=20,
             validation_split=0.1,
             )

   #保存と読み込み
   model.save("sincos_model.h5")
   load_model = load_model("sincos_model.h5")

   #予測
   lstm_data_y_predict = model.predict(lstm_data_x)

   plt.figure()
   plt.title('sin')
   plt.plot(lstm_data_y[:, 0], lw=2)
   plt.plot(lstm_data_y_predict[:, 0], '--', lw=2)
   plt.figure()
   plt.title('cos')
   plt.plot(lstm_data_y[:, 1], lw=2)
   plt.plot(lstm_data_y_predict[:, 1], '--', lw=2)

    #再帰予測
   lstm_data_future = pd.DataFrame(index=range(300), columns=['sin', 'cos'], data=0)
   lstm_data_future.iloc[:timesteps-1, :] = lstm_data_x[-1, :, :]

   for i in lstm_data_future.index[timesteps-1:]:

       x = lstm_data_future.iloc[i-timesteps+1:i, :].values.reshape(1, timesteps-1, -1)
       y = model.predict(x)
       lstm_data_future.iloc[[i], :] = y

   plt.figure()
   lstm_data_future.iloc[timesteps:].plot(title='future')