はじめに
Pythonで多項式近似を実施したいとき、一番簡単に使えるのはNumpyのPolyfit関数ではないでしょうか。ただ使っていてちょっと困ったのは、Excelでできるように、切片の値を0にできないこと。調べたのですが、Polyfitくらいお手軽にこれが設定できるものがありませんでした。そこで本記事では、numpyのpolyfitをちょっとだけ改造し、以下のようにfit_intercept(y切片を計算対象とするか)を指定できるようなファンクションに書き換える方法を記載します。
#fit_interceptをFalsenにすれば、y切片を0とした場合の値が返ってくる np.polyfit(x, y, 1, fit_intercept=False)
polyfitの普通の使い方
以下のような簡単なコードで、多項式近似を実行することができます。コードは下記サイト様のものをベースに作成しています。
pythonで近似式の計算
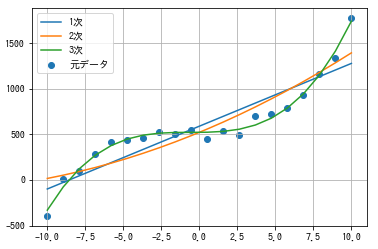
#ライブラリをインポート import numpy as np from matplotlib import pyplot as plt #適当にxとyを作成 x= np.linspace(-10, 10, 20) y= x**3 + 2*x**2 + 3*x + 500 + np.random.randn(20)*50 #近似式の係数 res1 = np.polyfit(x, y, 1) res2 = np.polyfit(x, y, 2) res3 = np.polyfit(x, y, 3) #近似式の計算 y1 = np.poly1d(res1)(x) #1次 y2 = np.poly1d(res2)(x) #2次 y3 = np.poly1d(res3)(x) #3次 #グラフ表示 plt.scatter(x, y, label='元データ') plt.plot(x, y1, label='1次') plt.plot(x, y2, label='2次') plt.plot(x, y3, label='3次') plt.grid() plt.legend() plt.show()
お手軽です。
fit_interceptのパラメータの追加
次にlib→site-package→numpy→libと進み、polynomial.pyを編集します。編集するのが怖い人は、バックアップを取っておくといいでしょう。
numpyのver.1.15であれば、393行目くらいにpolyfitという関数があるはずです。これを少しだけ、具体的には3か所書き換えていきます。
変更点①パラメータ追加
関数の定義部分に、fit_intercept=Trueという変数を追加します。Trueの場合には今まで同様y切片を計算し、Falseの場合にはy切片を0とした解を返すようにします。他のスクリプトに影響が出ないよう、デフォルトの値をTrue(今まで通り)としておきます。
元々
def polyfit(x, y, deg, rcond=None, full=False, w=None, cov=False):
"""
Least squares polynomial fit.
変更後
#fit_intercept=Trueを追加する。
def polyfit(x, y, deg, rcond=None, full=False, w=None, cov=False, fit_intercept=True):
"""
Least squares polynomial fit.
変更点②切片の計算要素を取り除く
次に560行目くらいまで下げていくと、lhs = vander(x, order)という行が見つかるはずです。これが多項式の説明変数を作っている部分ですので、この中にある定数項(一番右の行)を落とせばy切片を考慮しない計算ができます。そこで以下のように書き換えます。
元々
# set up least squares equation for powers of x lhs = vander(x, order) rhs = y
変更後
# set up least squares equation for powers of x
lhs = vander(x, order)
# fit_interceptがFalseの場合には一番右の列を計算対象から外す。
if fit_intercept == False:
lhs = lhs[:, :-1]
rhs = y
変更点③係数に切片0を加える
さらに580行目くらいまで下げていくと、係数cが計算されている行が見つかります。変更点②でy切片が計算されないようになったので、本来y切片が入る配列の一番最後に0.0を追加しましょう。
元々
# scale lhs to improve condition number and solve scale = NX.sqrt((lhs*lhs).sum(axis=0)) lhs /= scale c, resids, rank, s = lstsq(lhs, rhs, rcond) c = (c.T/scale).T # broadcast scale coefficients # warn on rank reduction, which indicates an ill conditioned matrix
変更後
# scale lhs to improve condition number and solve
scale = NX.sqrt((lhs*lhs).sum(axis=0))
lhs /= scale
c, resids, rank, s = lstsq(lhs, rhs, rcond)
c = (c.T/scale).T # broadcast scale coefficients
# fit_interceptがFalseの場合には配列の最後に0.0を足す。
if fit_intercept == False:
c = NX.asarray(c.tolist() + [0.0])
# warn on rank reduction, which indicates an ill conditioned matrix
これで修正は完了です。早速試してみましょう。
動作検証
先ほどのコードの近似式の計算の部分に、fit_intercept=Falseを指定します。
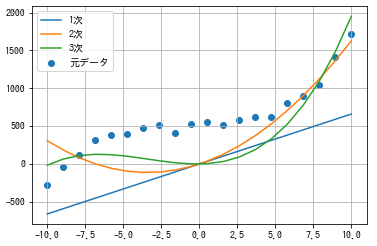
#ライブラリをインポート import numpy as np from matplotlib import pyplot as plt #適当にxとyを作成 x= np.linspace(-10, 10, 20) y= x**3 + 2*x**2 + 3*x + 500 + np.random.randn(20)*50 #近似式の係数(fit_intercept=Falseを指定) res1 = np.polyfit(x, y, 1, fit_intercept=False) res2 = np.polyfit(x, y, 2, fit_intercept=False) res3 = np.polyfit(x, y, 3, fit_intercept=False) #近似式の計算 y1 = np.poly1d(res1)(x) #1次 y2 = np.poly1d(res2)(x) #2次 y3 = np.poly1d(res3)(x) #3次 #グラフ表示 plt.scatter(x, y, label='元データ') plt.plot(x, y1, label='1次') plt.plot(x, y2, label='2次') plt.plot(x, y3, label='3次') plt.grid() plt.legend() plt.show()
各線が原点を通過するようになりました。
まとめ
interceptを0にできるpolyfit関数の改造方法を記載しました。Excelで簡単にできることがPythonでは難しいというのも悔しいので、こういった関数をどんどん活用していきたいですね。
ソースコード
polyfit部分を抜き出しておきます。
def polyfit(x, y, deg, rcond=None, full=False, w=None, cov=False, fit_intercept=True):
"""
Least squares polynomial fit.
Fit a polynomial ``p(x) = p[0] * x**deg + ... + p[deg]`` of degree `deg`
to points `(x, y)`. Returns a vector of coefficients `p` that minimises
the squared error.
Parameters
----------
x : array_like, shape (M,)
x-coordinates of the M sample points ``(x[i], y[i])``.
y : array_like, shape (M,) or (M, K)
y-coordinates of the sample points. Several data sets of sample
points sharing the same x-coordinates can be fitted at once by
passing in a 2D-array that contains one dataset per column.
deg : int
Degree of the fitting polynomial
rcond : float, optional
Relative condition number of the fit. Singular values smaller than
this relative to the largest singular value will be ignored. The
default value is len(x)*eps, where eps is the relative precision of
the float type, about 2e-16 in most cases.
full : bool, optional
Switch determining nature of return value. When it is False (the
default) just the coefficients are returned, when True diagnostic
information from the singular value decomposition is also returned.
w : array_like, shape (M,), optional
Weights to apply to the y-coordinates of the sample points. For
gaussian uncertainties, use 1/sigma (not 1/sigma**2).
cov : bool, optional
Return the estimate and the covariance matrix of the estimate
If full is True, then cov is not returned.
Returns
-------
p : ndarray, shape (deg + 1,) or (deg + 1, K)
Polynomial coefficients, highest power first. If `y` was 2-D, the
coefficients for `k`-th data set are in ``p[:,k]``.
residuals, rank, singular_values, rcond
Present only if `full` = True. Residuals of the least-squares fit,
the effective rank of the scaled Vandermonde coefficient matrix,
its singular values, and the specified value of `rcond`. For more
details, see `linalg.lstsq`.
V : ndarray, shape (M,M) or (M,M,K)
Present only if `full` = False and `cov`=True. The covariance
matrix of the polynomial coefficient estimates. The diagonal of
this matrix are the variance estimates for each coefficient. If y
is a 2-D array, then the covariance matrix for the `k`-th data set
are in ``V[:,:,k]``
Warns
-----
RankWarning
The rank of the coefficient matrix in the least-squares fit is
deficient. The warning is only raised if `full` = False.
The warnings can be turned off by
>>> import warnings
>>> warnings.simplefilter('ignore', np.RankWarning)
See Also
--------
polyval : Compute polynomial values.
linalg.lstsq : Computes a least-squares fit.
scipy.interpolate.UnivariateSpline : Computes spline fits.
Notes
-----
The solution minimizes the squared error
.. math ::
E = \\sum_{j=0}^k |p(x_j) - y_j|^2
in the equations::
x[0]**n * p[0] + ... + x[0] * p[n-1] + p[n] = y[0]
x[1]**n * p[0] + ... + x[1] * p[n-1] + p[n] = y[1]
...
x[k]**n * p[0] + ... + x[k] * p[n-1] + p[n] = y[k]
The coefficient matrix of the coefficients `p` is a Vandermonde matrix.
`polyfit` issues a `RankWarning` when the least-squares fit is badly
conditioned. This implies that the best fit is not well-defined due
to numerical error. The results may be improved by lowering the polynomial
degree or by replacing `x` by `x` - `x`.mean(). The `rcond` parameter
can also be set to a value smaller than its default, but the resulting
fit may be spurious: including contributions from the small singular
values can add numerical noise to the result.
Note that fitting polynomial coefficients is inherently badly conditioned
when the degree of the polynomial is large or the interval of sample points
is badly centered. The quality of the fit should always be checked in these
cases. When polynomial fits are not satisfactory, splines may be a good
alternative.
References
----------
.. [1] Wikipedia, "Curve fitting",
http://en.wikipedia.org/wiki/Curve_fitting
.. [2] Wikipedia, "Polynomial interpolation",
http://en.wikipedia.org/wiki/Polynomial_interpolation
Examples
--------
>>> x = np.array([0.0, 1.0, 2.0, 3.0, 4.0, 5.0])
>>> y = np.array([0.0, 0.8, 0.9, 0.1, -0.8, -1.0])
>>> z = np.polyfit(x, y, 3)
>>> z
array([ 0.08703704, -0.81349206, 1.69312169, -0.03968254])
It is convenient to use `poly1d` objects for dealing with polynomials:
>>> p = np.poly1d(z)
>>> p(0.5)
0.6143849206349179
>>> p(3.5)
-0.34732142857143039
>>> p(10)
22.579365079365115
High-order polynomials may oscillate wildly:
>>> p30 = np.poly1d(np.polyfit(x, y, 30))
/... RankWarning: Polyfit may be poorly conditioned...
>>> p30(4)
-0.80000000000000204
>>> p30(5)
-0.99999999999999445
>>> p30(4.5)
-0.10547061179440398
Illustration:
>>> import matplotlib.pyplot as plt
>>> xp = np.linspace(-2, 6, 100)
>>> _ = plt.plot(x, y, '.', xp, p(xp), '-', xp, p30(xp), '--')
>>> plt.ylim(-2,2)
(-2, 2)
>>> plt.show()
"""
order = int(deg) + 1
x = NX.asarray(x) + 0.0
y = NX.asarray(y) + 0.0
# check arguments.
if deg < 0:
raise ValueError("expected deg >= 0")
if x.ndim != 1:
raise TypeError("expected 1D vector for x")
if x.size == 0:
raise TypeError("expected non-empty vector for x")
if y.ndim < 1 or y.ndim > 2:
raise TypeError("expected 1D or 2D array for y")
if x.shape[0] != y.shape[0]:
raise TypeError("expected x and y to have same length")
# set rcond
if rcond is None:
rcond = len(x)*finfo(x.dtype).eps
# set up least squares equation for powers of x
lhs = vander(x, order)
if fit_intercept == False:
lhs = lhs[:, :-1]
rhs = y
# apply weighting
if w is not None:
w = NX.asarray(w) + 0.0
if w.ndim != 1:
raise TypeError("expected a 1-d array for weights")
if w.shape[0] != y.shape[0]:
raise TypeError("expected w and y to have the same length")
lhs *= w[:, NX.newaxis]
if rhs.ndim == 2:
rhs *= w[:, NX.newaxis]
else:
rhs *= w
# scale lhs to improve condition number and solve
scale = NX.sqrt((lhs*lhs).sum(axis=0))
lhs /= scale
c, resids, rank, s = lstsq(lhs, rhs, rcond)
c = (c.T/scale).T # broadcast scale coefficients
if fit_intercept == False:
c = NX.asarray(c.tolist() + [0.0])
# warn on rank reduction, which indicates an ill conditioned matrix
if rank != order and not full:
msg = "Polyfit may be poorly conditioned"
warnings.warn(msg, RankWarning, stacklevel=2)
if full:
return c, resids, rank, s, rcond
elif cov:
Vbase = inv(dot(lhs.T, lhs))
Vbase /= NX.outer(scale, scale)
# Some literature ignores the extra -2.0 factor in the denominator, but
# it is included here because the covariance of Multivariate Student-T
# (which is implied by a Bayesian uncertainty analysis) includes it.
# Plus, it gives a slightly more conservative estimate of uncertainty.
if len(x) <= order + 2:
raise ValueError("the number of data points must exceed order + 2 "
"for Bayesian estimate the covariance matrix")
fac = resids / (len(x) - order - 2.0)
if y.ndim == 1:
return c, Vbase * fac
else:
return c, Vbase[:,:, NX.newaxis] * fac
else:
return c