はじめに
その3では、「loto6で期待値の高い数値の選び方はあるのか?」について以下の手順で分析・解析していきます。
- 期待値の定義と算出
- 期待値を最大化する数字の選び方
なお、本記事ではその2の内容を踏まえて、「loto6で特別に出やすい数字はない(出目は完全にランダム)」という前提で進めていきます。
出目がランダムじゃ期待値を上げることなんて出来ないのではないか?と思うかもしれませんが、loto6は4等賞以上の当たりでは当選者で賞金を分配するシステムになっているため、人が選びにくい数字を選ぶことで期待値を上げられる可能性があります。仮説としては、例えば数字を誕生日等から選ぶ人が多ければ、月である1〜12、日である1〜31に選択される数字が集中するため、この範囲を選ばなければ当選が他人と被りにくく、期待値を上げられるというようなことがありえるのでは、と考えました。
期待値の定義と算出
期待値の定義
loto6は1口200円で購入することが出来るので、期待値とは「当選確率を考慮した当選金額が1口当たり何円か」であると言えます。また、この期待値が高くなるような数字の選び方を見つけ出すことが本記事の目的になります。
上記より、1口の期待値(E(1口))は以下の式で表すことが出来ます。
E(1口) = \Sigma_{k=1}^{5}{(k等賞の当選確率×k等賞の当選金額)}
\end{equation*}
期待値の算出
上記に示したとおり、期待値を算出するためには1〜5の各等賞の当選確率と当選金額を求める必要がありますので、以下順をおって算出していきます。
当選確率の理論値
loto6は1〜43の数字の中から6つの数字を選び、全て的中していれば1等賞、5つ的中していて残りの1つがボーナス数字と一致していれば2等賞、5つ的中していれば3等賞、4つ的中していれば4等賞、3つ的中していれば5等賞というように決まっていますのでそれぞれ以下のような式で理論値を求めることが出来ます。
p(1等賞) = \frac{{}_{6} C _6}{ {}_{43} C _6}
\end{equation*}
p(2等賞) = \frac{{}_{1} C _1 \cdot {}_{6} C _5 }{ {}_{43} C _6}
\end{equation*}
p(3等賞) = \frac{{}_{36} C _1 \cdot {}_{6} C _5 }{ {}_{43} C _6}
\end{equation*}
p(4等賞) = \frac{{}_{37} C _2 \cdot {}_{6} C _4 }{ {}_{43} C _6}
\end{equation*}
p(5等賞) = \frac{{}_{37} C _3 \cdot {}_{6} C _3 }{ {}_{43} C _6}
\end{equation*}
p(ハズレ|2個的中) = \frac{{}_{37} C _4 \cdot {}_{6} C _2 }{ {}_{43} C _6}
\end{equation*}
p(ハズレ|1個的中) = \frac{{}_{37} C _5 \cdot {}_{6} C _1 }{ {}_{43} C _6}
\end{equation*}
p(ハズレ|0個的中) = \frac{{}_{37} C _6 \cdot {}_{6} C _0 }{ {}_{43} C _6}
\end{equation*}
pythonのscipyを使って計算してみます。
import scipy.misc
import scipy as sp
#1等賞が当たる確率
sp.misc.comb(6, 6) / sp.misc.comb(43, 6)
#2等賞が当たる確率
sp.misc.comb(1, 1) * sp.misc.comb(6, 5) / sp.misc.comb(43, 6)
#3等賞が当たる確率
sp.misc.comb(36, 1) * sp.misc.comb(6, 5) / sp.misc.comb(43, 6)
#4等賞が当たる確率
sp.misc.comb(37, 2) * sp.misc.comb(6, 4) / sp.misc.comb(43, 6)
#5等賞が当たる確率
sp.misc.comb(37, 3) * sp.misc.comb(6, 3) / sp.misc.comb(43, 6)
#ハズレの確率
(sp.misc.comb(37, 4) * sp.misc.comb(6, 2) + sp.misc.comb(37, 5) * sp.misc.comb(6, 1) + sp.misc.comb(37, 6) * sp.misc.comb(6, 0)) / sp.misc.comb(43, 6)
整理すると下記のような感じです。5等すら2.5%程度しかなく、ほぼほぼ外れるギャンブルであることが分かります。
1等賞:およそ600万分の1
2等賞:およそ100万分の1
3等賞:およそ3万分の1
4等賞:およそ600分の1
5等賞:およそ40分の1
ハズレ:およそ40分の39
(参考)当選確率の実績値との比較
念の為、実データを使った当選確率の算出も実施してみます。データは以下で作ったものを使います。
import pandas as pd
#データ読み込み
df = pd.read_csv("loto6_allData.csv", index_col=1, parse_dates=True)
#データの上位5行を確認
df.head()
データには1等口数等の当選数があり、販売実績額を200(円/口)で割れば総口数が求まることから、これらを使って当選確率の実績値を求めることが可能です。
#総口数を計算
df['総口数'] = df['販売実績額'] / 200
#各等賞の割合を計算
for i in range(1, 6):
df[str(i)+'等割合'] = df[str(i)+'等口数'] / df['総口数']
#データ確認
df.iloc[:, -5:].head()
通算の平均値を計算してみます。
df[[str(i)+'等割合' for i in range(1, 6)]].mean()
先ほどの結果と比較してみましょう。
#理論値
percentList = [
sp.misc.comb(6, 6) / sp.misc.comb(43, 6),
sp.misc.comb(1, 1) * sp.misc.comb(6, 5) / sp.misc.comb(43, 6),
sp.misc.comb(36, 1) * sp.misc.comb(6, 5) / sp.misc.comb(43, 6),
sp.misc.comb(37, 2) * sp.misc.comb(6, 4) / sp.misc.comb(43, 6),
sp.misc.comb(37, 3) * sp.misc.comb(6, 3) / sp.misc.comb(43, 6),
]
#実績値
tdf = df[[str(i)+'等割合' for i in range(1, 6)]].mean()
#結合
tdf = pd.concat([tdf, pd.DataFrame(index=tdf.index, data=percentList)], axis=1)
tdf.columns = ['実績値', '理論値']
tdf['誤差率%'] = 100 * (tdf['実績値'] - tdf['理論値']).abs() / tdf['実績値']
#表示
tdf
ほぼ実績値と理論値が一致していますが、2等だけ15%程度違いがありますね。調べてみると、過去にドラマの数字と同じのを選ぶと2等が当選する!?というとんでもない事象があったようで、3等よりも多い3000口以上が当たったそうです。これは外れ値と考えられますので除外してもう一度見てみます。
https://www.news-postseven.com/archives/20120913_143230.html
#極端なケースを除外する
df = df[df['2等口数'] < 3000]
#実績値
tdf = df[[str(i)+'等割合' for i in range(1, 6)]].mean()
#結合
tdf = pd.concat([tdf, pd.DataFrame(index=tdf.index, data=percentList)], axis=1)
tdf.columns = ['実績値', '理論値']
tdf['誤差率%'] = 100 * (tdf['実績値'] - tdf['理論値']).abs() / tdf['実績値']
#表示
tdf
概ね一致してきましたね。loto6はほぼ理論通りの確率で当選者を出していると言えそうです。
各回での1口当たりの実績的な期待値の算出
理論通りの確率で当選するとして、当選確率は理論値を、当選金額は実績値を使うと、1回1回のloto6での期待値は以下のように計算できます。
E(1口) = \Sigma_{k=1}^{5}{(k等賞の当選確率×k等賞の当選金額)}
\end{equation*}
#数式に基づいて計算
df['1口の賞金期待値'] = 0
for i in range(1, 6):
df['1口の賞金期待値_' + str(i) + '等'] = df[str(i)+'等賞金'] * percentList[i-1]
df['1口の賞金期待値'] += df['1口の賞金期待値_' + str(i) + '等']
#表示
df['1口の賞金期待値'].head()
#統計量を確認
df['1口の賞金期待値'].describe()
平均的な期待値は102円で、200円に対してほぼ半減することが分かります。一方で、最大は230円と、期待値が1口の価格を上回ることもある、という結果です。高い期待値を狙う数字の選び方はあるのでしょうか。
期待値を最大化する数字の選び方
おおまかな傾向の確認
まず時系列的な変化を確認してみます。
%matplotlib inline
#単純に期待値をプロット
df['1口の賞金期待値'].plot()
#100点の移動平均をプロット
df['1口の賞金期待値'].rolling(100, center=True).mean().plot()
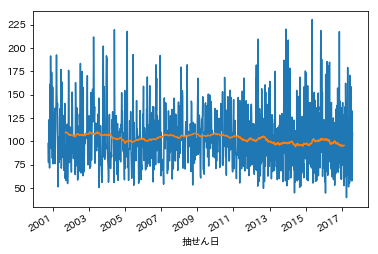
ばらつきは大きいですが、移動平均を取るとあまり全体としての傾向には差がないことが分かります。そのため、時期的に傾向が変わっているということはなさそうです。次にヒストグラムでばらつきの形状を見てみましょう。
df['1口の賞金期待値'].plot.hist()
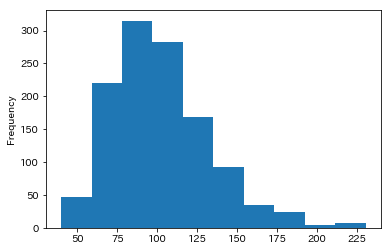
単峰性ですが歪んだ形状をしていることが分かります。特に、期待値が高くなる側にロングテールな傾向があります。期待値が高い5ケースと低い5ケースについて、データを確認してみましょう。
#期待値の上位5件
df.sort_values('1口の賞金期待値', ascending=False).iloc[:5].T
上位5件を見ると、2等の当選口数が少なく、2等の期待値が80円〜120円と非常に高いことが分かります。通常は中央値が100円程度ですので、この2等の期待値が全体の期待値を引っ張っているということのようです。また、当選数字を見ると、ボーナス数字を含めた当選数字に30とか40とかの大きい値が多いことが分かります。
#期待値の下位5件
df.sort_values('1口の賞金期待値').iloc[:5].T
下位5件を見ると、1等から4等までの期待値が非常に低いことが分かります。また、当選数字を見ると、5位を除き、当選数字に30未満の小さい数字が多いことが分かります。本当にカレンダーから数字を選ぶ人が多く期待値が上がりにくいのかもしれません。
次に特定の数字が出た時の期待値を計算してみましょう。具体的には1が出た時の期待値、2が出た時の期待値、という具合です。
tmp = []
#特定の数値が出た場合の期待値を計算する
for i in range(1, 44):
tmp.append(df[df[str(i)] >= 1][['1口の賞金期待値_' + str(i) + '等' for i in range(1, 6)] + ['1口の賞金期待値']].mean())
df_a = pd.concat(tmp, axis=1).T
df_a.index += 1
df_a.head()
1口の賞金期待値について棒グラフで確認してみましょう。
df_a['1口の賞金期待値'].plot.bar(figsize=(9, 6), ylim=(90, 120))
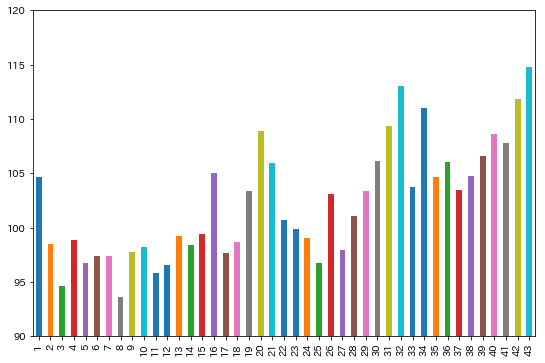
上位から43、32、42、34、31と大きい数字が並んでいることが分かります。逆に3や8はとても小さい傾向が読み取れます。これらは上の結果を裏付けるものであると言えます。一方で、20や21、16、1などの数字も高めの傾向があるようです。その2で見たように、1は最も出ていない、や、21は多め、等の傾向があるので、これらを元に戦略を練っている人の影響が出ているのかもしれません。
また、上記のグラフを等賞ごとの期待値の積み上げ棒グラフで描いた結果がこちら。
df_a[['1口の賞金期待値_' + str(i) + '等' for i in range(5, 0, -1)]].plot.bar(figsize=(9, 6), stacked=True)
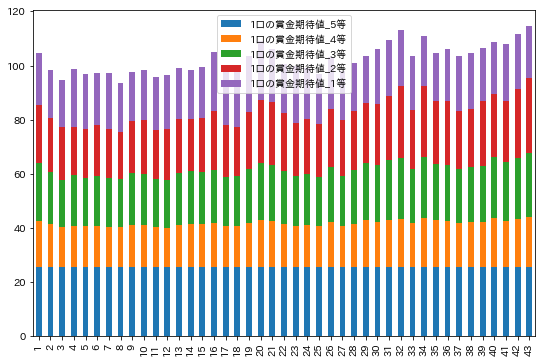
ぱっと見ですが、2等のばらつきが大きそうです。それぞれの標準偏差をプロットしてみましょう。
df_a[['1口の賞金期待値_' + str(i) + '等' for i in range(5, 0, -1)]].std().plot.bar(figsize=(9, 6), stacked=True)
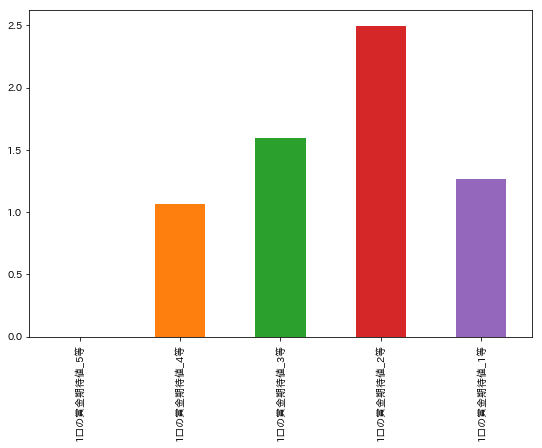
ばらつきは、2等、3等、1等、4等の順番のようです。これも上記の結果(上位5件は2等の期待値の影響が大きかった)を裏付けるものであると言えますね。
次にキャリーオーバーの額との関係を見てみましょう。
df.plot.scatter(x='キャリーオーバー_今回', y='1口の賞金期待値')
散布図では良くわからないですね。カテゴライズして集計してみましょう。
df['キャリーオーバー_今回_category'] = pd.cut(df['キャリーオーバー_今回'], 10)
df.pivot_table(index='キャリーオーバー_今回_category', values='1口の賞金期待値', aggfunc='median').plot.bar()
del df['キャリーオーバー_今回_category']
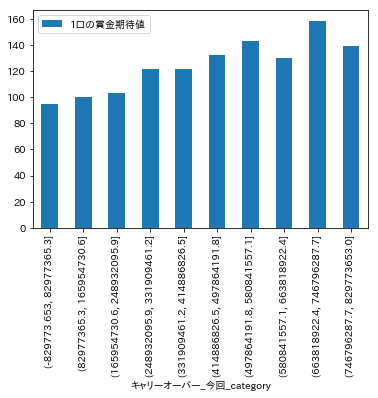
平均的には、キャリーオーバーが高いほど期待値も高くなる傾向が見て取れます。以上より、データの可視化により以下の傾向が見て取れました。
・ 期待値は時系列的にはほとんど変化していない
・ 期待値のばらつきは単峰性だが歪があり、高い側がなだらかな傾向がある
・ 期待値のばらつきの要因は特に2等賞の期待値が影響している
・ 当選番号に30以上の数字が多い場合は期待値が高く、それ以下の数字が多い場合には期待値が低い傾向がある
・ キャリーオーバーが高いほど期待値が高くなる傾向がある
決定木分析を用いた期待値の分析
さあ、とうとう本題に近づいてきました。決定木分析を使って期待値を分析してみます。
#必要なモジュールのインポート
from sklearn import tree
from sklearn.externals.six import StringIO
import pydotplus
from IPython.display import display, Image
説明変数として、本数字の値とボーナス数字、キャリーオーバーの金額、加えてそれぞれの数字が出たかどうかを与えます。
Exvar = df.columns[2:9].tolist() + df.columns[20:21].tolist() + df.columns[22:-12].tolist()
display(Exvar)
目的変数には1口の賞金金額の期待値を与えます。
#決定木で期待値を分析
clf = tree.DecisionTreeRegressor(max_depth=5)
clf.fit(df[Exvar], df[['1口の賞金期待値']])
学習結果の確認のため、feature_importanceを確認してみます。
pd.DataFrame(index=df[Exvar].columns, data=clf.feature_importances_).sort_values(0, ascending=False).head(10)
本数字4が最も影響し、次にキャリーオーバーが来ることが分かります。本数字4が来るということは、少なくとも値の大きい上位3つの数字の選び方が重要ということになります。(本数字5や6は必ず本数字4よりも大きい値になるため)
決定木を表示してみます。見やすさの都合で以下では深さ3までを表示しています。
# 決定木の描画
dot_data = StringIO() #dotファイル情報の格納先
tree.export_graphviz(clf, out_file=dot_data,
feature_names=df[Exvar].columns,
filled=True, rounded=True,
special_characters=True, max_depth=3)
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
Image(graph.create_png())

色が濃いほど期待値が高いことを示しています。これによると最も期待値が高いノード(右端)にたどり着くためには、
- 本数字4を31.5以上にする。(つまり、32以上から3つの数字を選ぶ)
- 本数字3を30.5以上にする。(つまり、31以上から4つの数字を選ぶ)
- 30が本数字の2番目以上の数字になっている。(つまり、30を含めて30以上から4つ又は5つの数字を選ぶ)
を満たすことが必要で、そのときはなんと期待値が180円!!まで上がることが分かります。通常の期待値は102円ですから、約倍まで上昇しています。またこの経路にはキャリーオーバーは関係ないというのもポイント(常にこの買い方をして良い)です。
また、その2つ隣にも期待値150円というルートがありますので見てみます。これにたどり着くためには、
- 本数字4を31.5以上にする。(つまり、32以上から3つの数字を選ぶ)
- 本数字3を30.5以下にする。(つまり、30以下から3つの数字を選ぶ)
- キャリーオーバーが約3億7千万円以上。
を満たすことが必要で、そのときは期待値が150円!まで上がることが分かります。通常の期待値は102円ですから、これも約1.5倍まで上昇しています。ただし、こちらはキャリーオーバが絡むので、いつもできる戦略ではないです。
上記の例では、30という特定の数字の有無が出てきて少し過学習の気配があるので、特定の数字は説明変数から除いたケースでも検討してみます。
Exvar = df.columns[2:9].tolist() + df.columns[20:21].tolist()
display(Exvar)
#決定木で期待値を分析
clf = tree.DecisionTreeRegressor(max_depth=5)
clf.fit(df[Exvar], df[['1口の賞金期待値']])
pd.DataFrame(index=df[Exvar].columns, data=clf.feature_importances_).sort_values(0, ascending=False).head(10)
特定の数字を除いたことにより、feature_importanceの傾向も少し変わっています。決定木も見ていきます。
# 決定木の描画
dot_data = StringIO() #dotファイル情報の格納先
tree.export_graphviz(clf, out_file=dot_data,
feature_names=df[Exvar].columns,
filled=True, rounded=True,
special_characters=True, max_depth=3)
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
Image(graph.create_png())
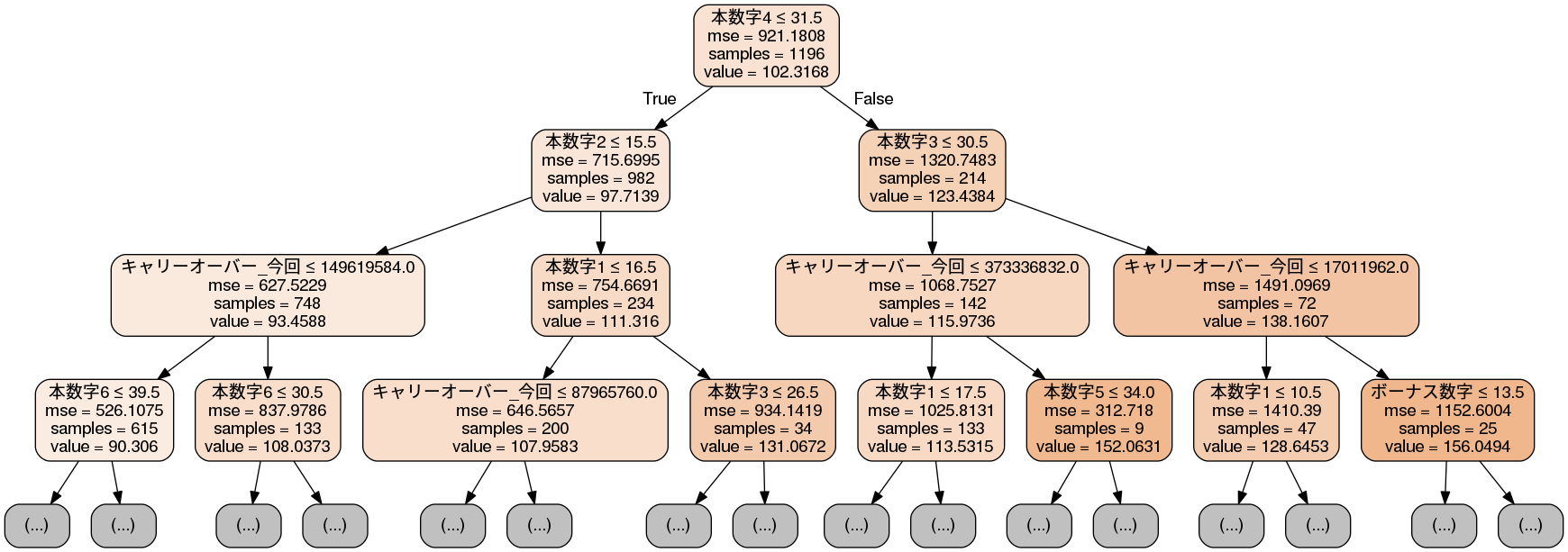
これによると最も期待値が高いノード(右端)にたどり着くためには、
- 本数字4を31.5以上にする。(つまり、32以上から3つの数字を選ぶ)
- 本数字3を30.5以上にする。(つまり、31以上から4つの数字を選ぶ)
- キャリーオーバーが約1億7千万円以上。
を満たすことが必要で、そのときは期待値が160円程度まで上がることが分かります。通常の期待値は102円ですから、これも約1.5倍まで上昇しています。これもキャリオーバーが絡む買い方ですね。それ以外に関しては、あまり形状に変化がなさそうです。
上記をまとめると、1口当たりの期待値を上げるための数字の選び方として、以下のことが言えそうです。
・ なるべく大きい数字から選ぶ。具体的には、①32以上から3つ以上、又は②31以上から4つ以上の数字を選ぶ。
・ キャリーオーバの額が多い時を狙う。①の時は約4億円、②の時は約2億円以上あれば期待値は約1.5倍(1口当たり150円程度)まで上がる。
・ 過学習気味だが、②の時にさらに30を選んでいると期待値が180円!まで跳ね上がる可能性もある。
まとめ
本記事では、「loto6で期待値の高い数値の選び方はあるのか?」について分析を実施しました。当初の予想が当たっていたのか、決定木分析等で得られたルールを見ると、予想以上に(1〜31)から数字を選ばないほうがいいという結果になっており、裏を返せばカレンダ情報等から数字を選ぶ方が多い傾向が見て取れました。loto6は当選者数が少ないほど賞金が増えるシステムのですので、loto6で損をしにくくするためには、カレンダ情報から数字を選ぶときは多くとも3個まで、という考えが必要そうです。
とはいえ、期待値が上がると言っても1口の費用(200円)を超えるわけではありませんので、買えば買うほど損をしてしまうことは変わりませんので、ギャンブルはほどほどに、楽しんで遊べるといいですね!