概要¶

Pythonを使って音楽ファイルを読み込み、サウンドスペクトログラムを作る手順を整理しました。大まかな手順は以下です。

pydubを使って音楽ファイルを読み込み

numpyを使ってフーリエ変換を実施し、スペクトログラムを作成

matplotlibとseabornでスペクトログラムを可視化

サウンドスペクトログラムとは以下のような横軸時間、縦軸周波数スペクトルをとったヒートマップです。

スペクトログラムって何？ということについては↓このあたりがイメージつかみやすいかと思います。
http://blog.media.teu.ac.jp/2015/05/post-0ec1.html
音声ファイルはスーパーマリオ64のウォーターランドの曲を使わせていただきました。

https://www.nintendo.co.jp/ds/series/dsi/menu/sound/download.html

以下のモジュールをインポートしておきます。（ない場合にはpip等でインストールおねがいします）

In [1]:

from pydub import AudioSegment
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

%matplotlib inline

なお、pydubを使うにはffmpegが必要になるので、準備しておきましょう。以下記事等を参考にしてみてください。
Pythonのmatplotlibでgifアニメを作成する

pydubを使って音楽ファイルを読み込み¶

読み込みは以下１行で実行できます。以下例ではm4aを対象にしていますが、mp3やwav等でも同様のコード（m4a部分を変える）で読み込むことができるはずです。

In [2]:

sound = AudioSegment.from_file("ウォーターランド.m4a", "m4a")

基本情報は以下で取得できます。
https://qiita.com/itoru257/items/8af2902d8ce851ae74ea

In [3]:

#チャンネル数(1:mono, 2:stereo)
sound.channels

Out[3]:

In [4]:

#サンプルレート(Hz)
sound.frame_rate

Out[4]:

In [5]:

#再生時間(秒)
sound.duration_seconds

Out[5]:

55.72643990929705

get_array_of_samplesを使うことで、生データをListで受け取ることができます。後々のことを考えて、numpyで読み込み、加えてステレオ音声から片側だけの音を抽出しておきます。

In [6]:

samples = np.array(sound.get_array_of_samples())
sample = samples[::sound.channels]

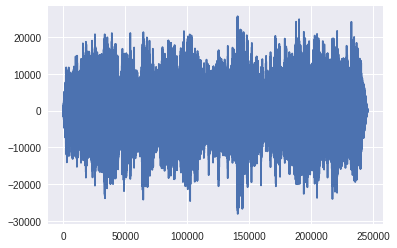
簡単にプロットするとこんな感じ。

In [7]:

plt.plot(sample[::10])

Out[7]:

[<matplotlib.lines.Line2D at 0x7f29b2aaa518>]

numpyを使ってフーリエ変換を実施し、スペクトログラムを作成¶

まずはスペクトルを計算してみる¶

フーリエ変換はnumpyの機能を使って簡単に実施することができます。
https://docs.scipy.org/doc/numpy-1.13.0/reference/routines.fft.html

In [8]:

#フーリエ変換自体は以下１行を実行するだけ
spec = np.fft.fft(sample)

In [9]:

#スペクトルの値（複素数）が入っている。
spec

Out[9]:

array([ 909365.00000000     +0.j        ,
         51629.03247526+667871.8941476j ,
       -461312.87203113-154156.11920285j, ...,
        335244.22709894+308623.48241612j,
       -461312.87203112+154156.11920289j,   51629.03247527-667871.89414759j])

スペクトル（複素数）の取り扱いを簡単に列挙しておきます。

In [10]:

#実数部分を取り出し
spec.real

Out[10]:

array([ 909365.        ,   51629.03247526, -461312.87203113, ...,
        335244.22709894, -461312.87203112,   51629.03247527])

In [11]:

#虚数部分を取り出し
spec.imag

Out[11]:

array([      0.        ,  667871.8941476 , -154156.11920285, ...,
        308623.48241612,  154156.11920289, -667871.89414759])

In [12]:

#絶対値を取り出し
np.abs(spec)

Out[12]:

array([ 909365.        ,  669864.48180705,  486388.39931611, ...,
        455672.19105605,  486388.39931612,  669864.48180704])

In [13]:

#偏角を取り出し
np.angle(spec)

Out[13]:

array([ 0.        ,  1.49364597, -2.81909085, ...,  0.74407664,
        2.81909085, -1.49364597])

In [14]:

#絶対値と偏角から複素数を復元
np.exp(1j*np.angle(spec))*np.abs(spec)

Out[14]:

array([ 909365.00000000     +0.j        ,
         51629.03247526+667871.8941476j ,
       -461312.87203113-154156.11920285j, ...,
        335244.22709894+308623.48241612j,
       -461312.87203112+154156.11920289j,   51629.03247527-667871.89414759j])

In [15]:

#逆変換
np.fft.ifft(spec)

Out[15]:

array([  1.00000000e+00 -3.23473530e-12j,
         1.00000000e+00 -2.99057462e-12j,
         1.00000000e+00 -1.14700955e-12j, ...,
        -1.21269118e-11 -6.54196579e-12j,
        -9.99257535e-12 -7.04638408e-12j,  -1.04776518e-11 -7.39542712e-12j])

In [16]:

#周波数
np.fft.fftfreq(sample.shape[0], 1.0/sound.frame_rate)

Out[16]:

array([ 0.        ,  0.0179448 ,  0.03588961, ..., -0.05383441,
       -0.03588961, -0.0179448 ])

In [17]:

#スペクトルをプロット表示
freq = np.fft.fftfreq(sample.shape[0], 1.0/sound.frame_rate)
plt.plot(freq, np.abs(spec))

Out[17]:

[<matplotlib.lines.Line2D at 0x7f29b2986c50>]

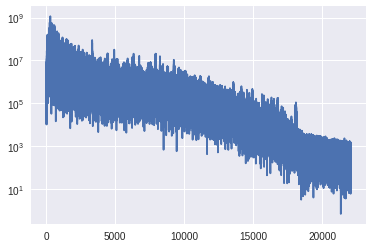
負の領域は使わないことや、周波数0の値が２倍されていること、対数メモリのほうが見やすことに留意して以下のように表示します。

In [18]:

freq = freq[:int(freq.shape[0]/2)]
spec = spec[:int(spec.shape[0]/2)]
spec[0] = spec[0] / 2

#plt.xscale("log")
plt.yscale("log")
plt.plot(freq, np.abs(spec))

Out[18]:

[<matplotlib.lines.Line2D at 0x7f29b28fbef0>]

どうやら100〜1000Hzのスペクトルが強いことが分かりました。

スペクトログラムを作成¶

上では全体の波形を使って１つのスペクトルを算出しましたが、これを一定の幅を取り、それを刻み幅ずつ動かしながら算出していくことでスペクトログラムが作成できます。

In [19]:

#窓幅
w = 1000
#刻み
s = 500

In [20]:

#スペクトル格納用
ampList = []
#偏角格納用
argList = []

#刻みずつずらしながら窓幅分のデータをフーリエ変換する
for i in range(int((sample.shape[0]- w) / s)):
    data = sample[i*s:i*s+w]
    spec = np.fft.fft(data)
    spec = spec[:int(spec.shape[0]/2)]
    spec[0] = spec[0] / 2
    ampList.append(np.abs(spec))
    argList.append(np.angle(spec))

#周波数は共通なので１回だけ計算（縦軸表示に使う）  
freq = np.fft.fftfreq(data.shape[0], 1.0/sound.frame_rate)
freq = freq[:int(freq.shape[0]/2)]

#時間も共通なので１回だけ計算（横軸表示に使う）
time = np.arange(0, i+1, 1) * s / sound.frame_rate

#numpyの配列にしておく
ampList = np.array(ampList)
argList = np.array(argList)

上記でスペクトログラムのデータを作成することができました。

matplotlibとseabornでスペクトログラムを可視化¶

次に実際に可視化をしていきます。

In [21]:

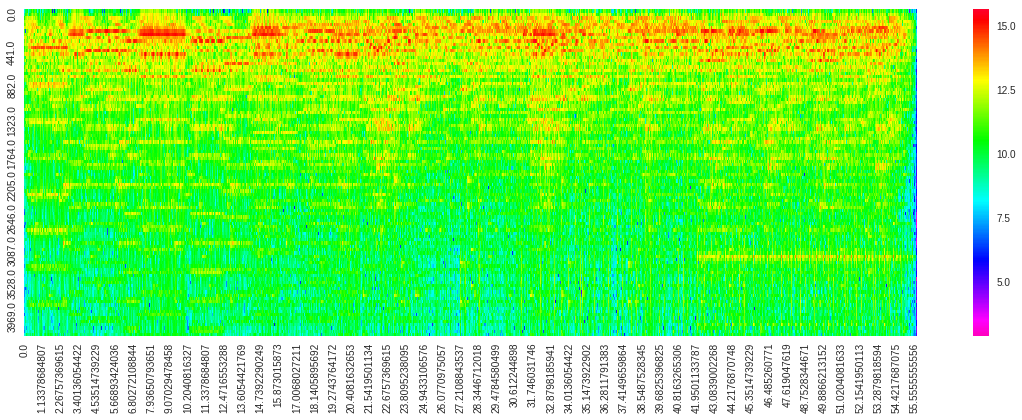
df_amp = pd.DataFrame(data=ampList, index=time, columns=freq)

In [22]:

#seabornのheatmapを使う
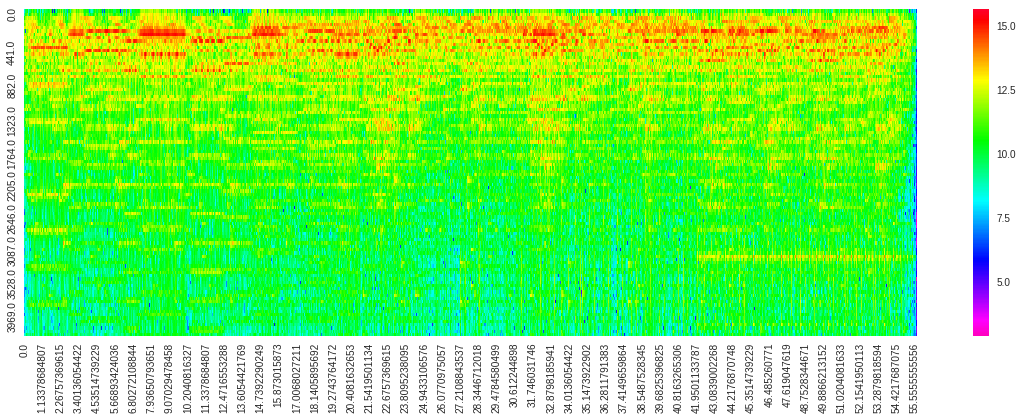
plt.figure(figsize=(20, 6))
sns.heatmap(data=np.log(df_amp.iloc[:, :100].T), 
            xticklabels=100, 
            yticklabels=10, 
            cmap=plt.cm.gist_rainbow_r,
           )

Out[22]:

<matplotlib.axes._subplots.AxesSubplot at 0x7f29b262c438>

100Hz〜500Hzくらいが高いという、かなりはっきりした傾向がありますね。

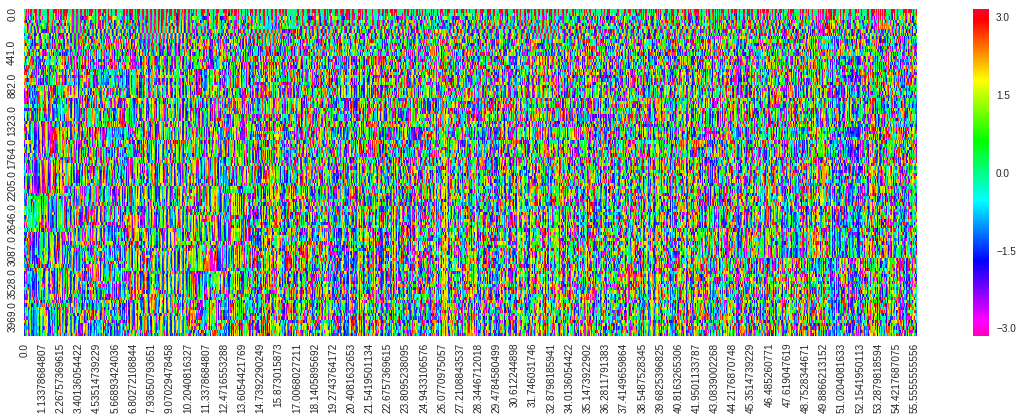
偏角の方も可視化してみます。

In [23]:

df_arg = pd.DataFrame(data=argList, index=time, columns=freq)

In [24]:

plt.figure(figsize=(20, 6))
sns.heatmap(data=df_arg.iloc[:, :100].T, 
            xticklabels=100, 
            yticklabels=10, 
            cmap=plt.cm.gist_rainbow_r,
           )

Out[24]:

<matplotlib.axes._subplots.AxesSubplot at 0x7f29b26c8c88>

こちらはほぼランダムに見えますね。それとも、スペクトルと何か相関があるのでしょうか。

まとめ¶

ちょっと今さから感もありますが、Pythonでサウンドスペクトログラムを作ってみました。引き続き、スペクトルと偏角に関係があるかどうか検討していこうと思います。

自調自考の旅

Pythonを使ったデータ分析を実施したい方や、実施している方の役に立つ記事を書いていきます！

Pythonを使って音声データからスペクトログラムを作成する

概要¶

pydubを使って音楽ファイルを読み込み¶

numpyを使ってフーリエ変換を実施し、スペクトログラムを作成¶

まずはスペクトルを計算してみる¶

スペクトログラムを作成¶

matplotlibとseabornでスペクトログラムを可視化¶

まとめ¶

コメントを残すコメントをキャンセル

概要¶

pydubを使って音楽ファイルを読み込み¶

numpyを使ってフーリエ変換を実施し、スペクトログラムを作成¶

まずはスペクトルを計算してみる¶

スペクトログラムを作成¶

matplotlibとseabornでスペクトログラムを可視化¶

まとめ¶

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル