#Pandasを用いてデータを読み込み、データフレームに格納します。
import pandas as pd
df = pd.read_csv("loto6.csv", encoding="cp932", parse_dates=[1])
#抽選番号に係るデータだけを使う
df = df.iloc[:, 3:10]
#データ確認
df.head()

#まずはpandasのmeltを用いて数値を1列の項目に変換
df = pd.melt(df)
#データ確認
df.head()

#次にpivot-tableを用いて数値ごとの抽選回数を算出
df = pd.pivot_table(df, index='value', aggfunc='count')
df.columns = ['frequency']
#データ確認
df.head()

#棒グラフで可視化
%matplotlib inline
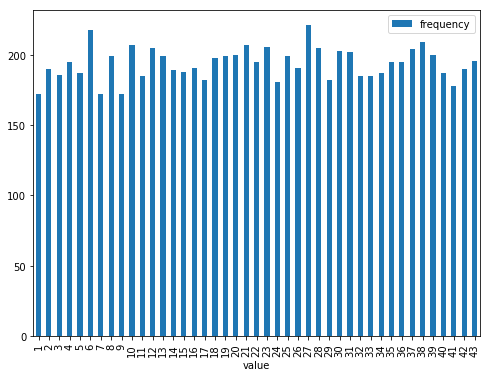
df.plot.bar(figsize=(8, 6))

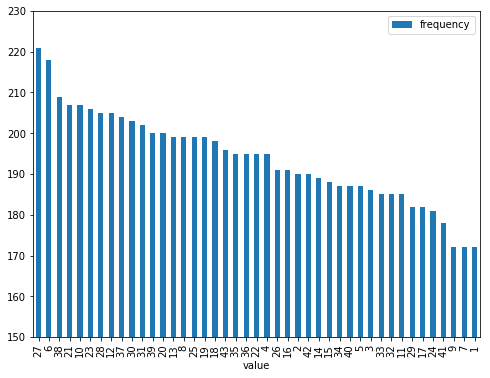
df.sort_values('frequency', ascending=False).plot.bar(ylim=[150, 230], figsize=(8, 6))

#ヒストグラムをプロット
df.plot.hist(bins=7)

#平均と標準偏差を計算
print("平均：" + "{0:.3f}".format(df.mean().values[0]))
print("標準偏差：" + "{0:.3f}".format(df.std().values[0]))

#loto6のデータフレームを受け取り、平均と標準偏差を返すファンクション
#dfがデータフレーム、iは開催回数を表す。
def getdistInfo(df, i):
    
    #指定した開催日までのデータを抽出
    df = df.ix[:i]
    
    #andasのmeltを用いて数値を1列の項目に変換
    df = pd.melt(df)
    
    #pivot-tableを用いて数値ごとの抽選回数を算出
    df = pd.pivot_table(df, index='value', aggfunc='count')
    df.columns = ['frequency']
    
    #分布の平均と標準偏差を返す
    return df.mean().values[0], df.std().values[0]

#データフレームを読み直す
tdf = pd.read_csv("loto6.csv", encoding="cp932", parse_dates=[1])
df = tdf.iloc[:, 3:10]

result = []
for i in df.index:
    result.append(getdistInfo(df, i))
    
result = pd.DataFrame(result, columns=['mean', 'std'], index=tdf['抽せん回'])
result.index.name = 'times'

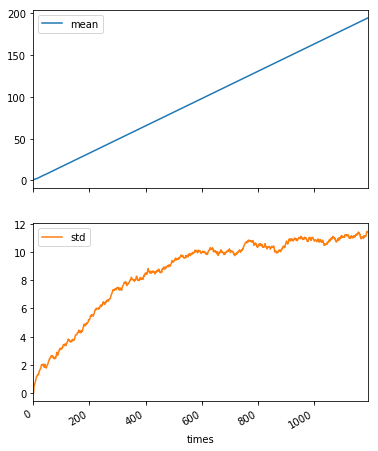
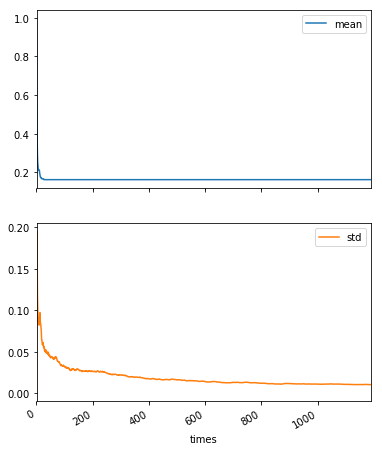
result.plot(subplots=True, figsize=(6, 8))

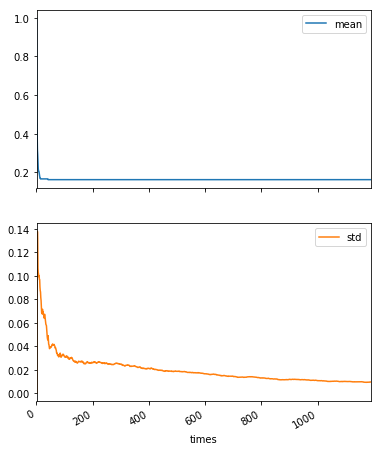
(result.T / result.index.values).T.plot(subplots=True, figsize=(6, 8))

#numpyを使ってモンテカルロシミュレーション
import numpy as np

#プログラムに再現性を持たせるため乱数のシードを設定
np.random.seed(0)

#1～43の数字から重複なしで7つの数字を選択
data = np.random.choice(range(1, 44), replace=False, size=7)
data.sort()

#結果確認
print(data)

datas = []
numbers = list(range(1, 44))
np.random.seed(0)

for i in df.index:
    data = np.random.choice(numbers, replace=False, size=7)
    data.sort()
    datas.append(data)
    
vloto6 = pd.DataFrame(datas, index=df.index, columns=df.columns)

#結果確認
vloto6.head()

vresult = []
for i in df.index:
    vresult.append(getdistInfo(vloto6, i))
    
vresult = pd.DataFrame(vresult, columns=['mean', 'std'], index=tdf['抽せん回'])
vresult.index.name = 'times'

(vresult.T / vresult.index.values).T.plot(subplots=True, figsize=(6, 8))

#シミュレーションを青、実際を赤で描画
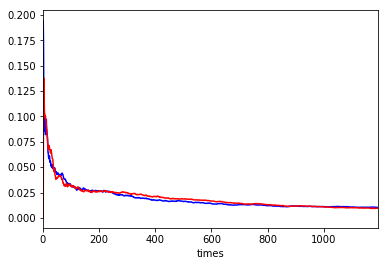
ax = (vresult.T / vresult.index.values).T['std'].plot(c='b')
(result.T / result.index.values).T['std'].plot(c='r', ax=ax)

#loto6のデータフレームを受け取り、標準偏差の時系列変化を返すファンクション
#dfがloto6の実際の結果の抽出番号のデータフレーム、tdfはそれ以外も含めたもの。jは乱数のシードを表す。
def loto6simulation(df, tdf, j):
    
    #仮想的なloto6の結果を作成
    datas = []
    numbers = list(range(1, 44))
    np.random.seed(j)

    for i in df.index:
        data = np.random.choice(numbers, replace=False, size=7)
        data.sort()
        datas.append(data)

    vloto6 = pd.DataFrame(datas, index=df.index, columns=df.columns)
    
    #時系列的な標準偏差の変化を算出
    vresult = []
    for i in df.index:
        vresult.append(getdistInfo(vloto6, i))

    vresult = pd.DataFrame(vresult, columns=['mean', 'std'], index=tdf['抽せん回'])
    vresult.index.name = 'times'
    
    return (vresult.T / vresult.index.values).T['std']

#ライブラリのインポート
from joblib import Parallel, delayed

#これがないとjoblibが止まるので入れておく
if __name__ == "__main__":
    #n_jobsがコア数
    vresults = Parallel(n_jobs=1, verbose=1)([delayed(loto6simulation)(df, tdf, j) for j in range(100)])
    
    #concatを使って結合
    vresults = pd.concat(vresults, axis=1)
    
    #結果確認
    vresults.head()

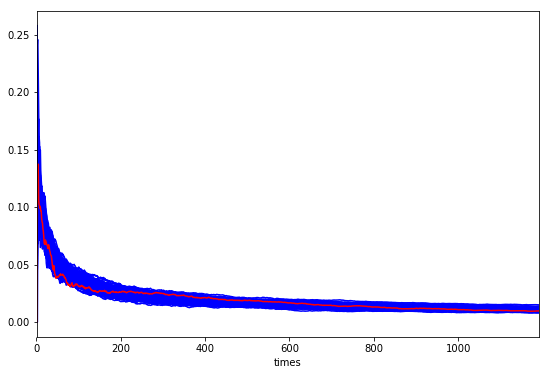
ax = vresults.plot(legend=False, c='b', figsize=(9, 6))
(result.T / result.index.values).T['std'].plot(c='r', ax=ax)